Holografik ilke nedir ve neden içinde yaşadığımız evrenin gerçek olmadığı anlamına gelmez?
Holografi ilkesi, en özet haliyle, evrende seçilecek bir hacim içerisinde var olabilecek enformasyon miktarının üst limitinin bu hacim ile değil, hacme ait yüzey alanı ile orantılı olduğudur. Yani, 3 boyutlu bir hacmin içindekileri tarif etmek için, 2 boyutlu bir yüzey yeterlidir. Başka bir deyişle, ikisi birbirine eşdeğerdir; aynı durumun iki ayrı tasviridir. Bu durum, 2 boyutlu yüzeyler ile 3 boyutlu görsellerin oluşturulduğu hologramlara benzer. Benzerlik burada bitiyor, ancak tartışmalar buradan sonra başlıyor.
Özellikle sosyal medyadaki tartışmalarda, holografik ilke ve simülasyon hipotezi, birbirine çorba edilerek “kesin Matrix’te yaşıyoruz” gibisinden ifadeler ile karşılaşmanız mümkün. Bu tür yanlış anlamaların önemli nedenleri arasında, bilim insanları tarafından kullanılan kavramların doğru karşılıklarının bilinmemesi, yapılan benzetmelerin kelime anlamlarıyla alınması ve kimi zaman oldukça karmaşık olan matematiksel anlatımlarının ise olduğu gibi göz ardı edilmesi sayılabilir.

Teorik olarak: Herkes kendi kendisinin dedesi ve android, hepimiz Matrix’deyiz, ayrıca ne olduğunu bilmediğimiz her şeyin sorumlusu Illuminati
Kavramların yanlış kullanımı, örneğin, holografi ilkesi için “holografik evren teorisi” gibi aslında var bile olmayan kullanımlar yaratabiliyor. Bir “teori olduğu” gerekçesiyle, teorilere toptan inanmayanlarla, bilimde adı olan her şeyi “teori” zannedenler arasında sonu gelmeyen ve bir yere varamayacak tartışmalara neden oluyor. Eğer siz de bazı genel kavramlarla ilgili bilginizi tazelemek isterseniz, “Teori, ‘sonuçta yalnızca bir teori’ midir? Yoksa durum biraz daha karışık mı?” yazısına bir göz atabilirsiniz.
Teori, “sonuçta yalnızca bir teori” midir, yoksa durum biraz daha karışık mı?
Peki ama, holografik ilke nereden çıktı; neden enformasyon ile yüzeyler ve hacimler arasında bazı bağıntılara ihtiyaç duyuldu?
Einstein, 1905 yılında yayımladığı Özel Görelilik Teorisi ile iki şey söyledi. Birincisi, fizik kanunları ivmeli hareket içinde olmayan tüm gözlemciler için aynıdır; ve ikincisi, ışığın boşluktaki hızı, hangi hızla hareket ederlerse etsinler, tüm gözlemciler için aynıdır. Bundan on yıl sonra yayımladığı Genel Görelilik ile de, özel görelilik ile Newton’un evrensel kütleçekim kanununu birleştirerek, kütleçekiminin, uzay-zamanın geometrik bir özelliği olduğunu; yani uzay-zamana ait eğriliğinin, içerisinde bulunan enerji, momentum, kütle ve ışıma kaynakları tarafından belirlendiğini söyleyen Einstein Alan Denklemleri’ni ortaya koydu. (1)
Einstein’ın yayınından yalnızca birkaç ay sonra, Karl Schwarzchild tarafından, Einstein alan denklemlerine ait ilk çözüm bulundu. Bu çözüm bulunur bulunmaz, karadeliklere ait olduğu düşünülmedi, hatta kara deliklerin varlığı genel olarak 20. yy’ın ikinci yarısında kabul gördü denebilir.

Karadelikler konusunda doktora seviyesinde bilgi sahibi olmak için Intersatellar’ı izlemeniz yeterli, hatta fazla bile
Schwarzchild’in çözümü, vakum için, noktasal bir kütlenin etrafında, açısal momentumu ve elektrik yükü olmayan ve küresel simetrik olan karadelikler için geçerlidir. Küresel koordinatlardaki Schwarzchild çözümü aşağıdaki şekildedir:
$$ds^2=-(1-\frac{r_s}{r})c^2 dt^2+\frac{dr^2}{1-\frac{r_s}{r}}+r^2(d\theta^2+sin^2\theta d\phi^2) \quad\quad\text{(d.1)}$$
$$r_s=\frac{2GM}{c^2} \quad\quad\text{(d.2)}$$
Burada ds2 uzay zaman aralığı, rs, Schwarzchild yarıçapı, r küreye olan uzaklık, c ışık hızı, ϴ polar açı ve φ azimutal açı, G evrensel kütleçekim sabiti ve M, karadeliği oluşturan cisim(ler)e ait kütledir (2, 3). Burada, karadeliğin merkezine doğru açısal hareket yapmadan hareket eden bir gözlemci varsayarak, açısal terimleri ihmal edebiliriz.
Şimdi, (d.1)’deki tekillik noktalarına, yani denklemin sonsuza gittiği noktalara bakarsak, iki tekillik noktası ortaya çıkar. Bunlardan ilki rs/r=1 ve dolayısı ile 1/(1-rs/r) teriminin sonsuza gittiği noktadır; bu nokta, karadeliğe ait “olay ufku”nu göstermektedir. Bu noktadaki tekilliğin, koordinat seçiminden kaynaklandığı, sonradan gösterilmiştir (4). Ancak noktanın özelliği, buradan itibaren uzay-zaman aralığı yalnızca tek tarafa doğru akabilir. Yani, olan ufkunu geçen bir gözlemci, karadeliğin merkezindeki tekilliğe doğru gitmek zorundadır. (5)
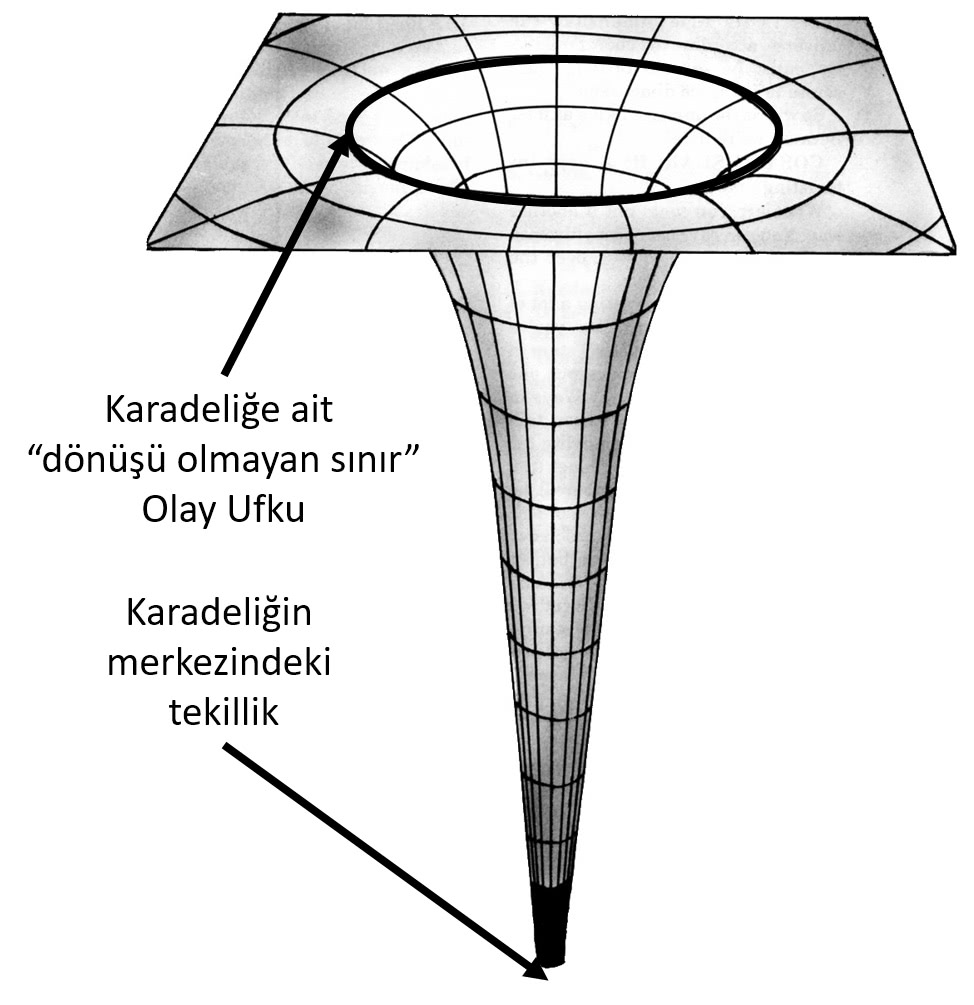
Karadeliğin, uzay-zamanda yarattığı eğrilik
Diğer taraftan, karadeliğin merkezinde bulunan, yani r=0 noktasındaki tekilliğin ise, koordinat seçiminden bağımsız olduğu gösterilmiştir. Bu nedenle bu noktadaki tekilliğe, “gerçek bir tekillik”tir denir. Bu nokta, karadeliğin merkezindeki, kütleçekiminin ve yoğunluğun sonsuza gittiği noktadır (4).
Olay ufku, kaçış hızının, ışık hızına eşit olduğu nokta veya uzay zamanın bir artık bir dışarısı olmayacak kadar kendi içine büküldüğü bir nokta, veya uzay koordinatlarıyla, zaman koordinatlarının rollerini değiştirdikleri nokta olarak düşünmek mümkün. Bu, her şekilde, ışığın dahil, olay ufkunu geçen herhangi bir cismin geri dönemeyeceği noktalar olduğu anlamına geliyor. Yani olay ufkunu geçen herhangi bir şey, evren açısından sonsuza kadar kayboluyor gibi görünüyor.
Ancak yukarıdaki klasik yaklaşım doğrultusunda, karadelik dışındaki bir gözlemci için, karadeliğe doğru giden cisim, karadeliğe “asimptotik” olarak yaklaşır. Yani sonsuz zaman sonra hala olay ufku üzerinde donmuş olarak kalır. Bu klasik yaklaşım açısından birincisi, karadeliğe düşen cismin hiçbir önemi yoktur, ikincisi karadeliğe bu şekilde düşecek cisimlerin miktarında herhangi bir sınırlama yoktur. Sonsuz miktarda cisim, olay ufkunda asılı kalabilir, bunun bir üst limiti yoktur (6). Ancak karadeliğin içeri doğru çekimi nedeniyle, olay ufkunda asılı kalan cisimlerin yaydığı ışığın dalga boyu, giderek daha fazla kırmızıya doğru kayar ve en sonunda tespit edilemez hale gelir.
Fakat, görelilik teorisi için, termodinamik yasaları sınırlayıcı değildir, ve yukarıdaki çizilen resim, karadeliğe ait olay ufkunda, sonsuz miktarda cismin asılı kalabileceğini söyleyerek, hem termodinamiğin ikinci yasası olan, entropinin her zaman artacağı ilkesi hem de enformasyonun (yani entropinin) kuantum alanları teorisine göre hiçbir zaman yok olmayacağı ilkeleri ile çelişir. Bu nedenle, 1972 yılında, Jacob Bekenstein, ne kadar entropisi olacağını hesaplamaya çalışmış ve karadeliğin entropisinin, olay ufkunun alanı ile orantılı olduğunu göstermiştir (7).
Bekenstein’ın düşünce çizgisi, Leonard Susskind tarafından, özetle şu şekilde anlatılmaktadır (6): Her defasında tek parçacık göndererek, sıfırdan bir karadelik oluşturmaya çalışalım; yani karadeliğe her defasında yollayacağımız 1 bitlik enformasyonun (yani foton var mı, yok mu?), karadelikte ne gibi bir değişime neden olacağına bakalım. Ancak yollayacağımız fotonun dalga boyu, enformasyonun 1 bit olabilmesi için, karadeliğin büyüklüğü ile orantılı olsun; aksi takdirde, “yalnızca foton var mı, yok mu?” bilgisinin yanında, “foton karadeliğin neresinde?” gibi daha fazla bilgi yollamış oluruz. Bu nedenle:
$$r_s=\lambda \quad\quad\text{(d.3)}$$
Burada rs, karadeliğe ait olay ufkunun çapı, λ ise gönderilen fotonun dalga boyudur. E = m c2‘den, ve Compton dalga boyu bağıntılarından (8), her defasında karadelik içerisine gönderilen enerji aşağıdaki gibidir:
$$\delta E = \frac{\hbar c}{2\pi r_s} \quad\quad\text{(d.4)}$$
Bu durumda, bu kadarlık enerjinin yarattığı kütle değişimi ise aşağıdaki gibidir:
$$\delta M = \frac{\hbar c}{2\pi r_s c} \quad\quad\text{(d.5)}$$
Bu değeri, (d.2)’de verilen Schwarzchild yarıçapı bağıntısında yerine koyarsak:
$$\delta r_s = \frac{2G}{c^2}\frac{\hbar c}{2\pi r_s} \quad\quad\text{(d.6)}$$
Burada, bir alan bağıntısı ortaya çıkmaktadır;
$$\delta A = r_s\delta r_s = \frac{\hbar G}{\pi c^3} \quad\quad\text{ (d.7)}$$
Yani, bir karadelik içine gönderilen parçalar, olay ufkunun kapladığı hacmi değil, olay ufkunun yüzey alanını doğrudan etkilemektedir. Bu, içinde bulunduğumuz evren için, seçilen bir yerde var olabilecek enformasyon miktarı için bir üst limittir (6, 8).
Ancak, entropi konusunda bulunan bu üst sınıra rağmen, 1975 yılında Stephen Hawking, Bekenstein’a ait konjektürü de kullanarak, karadeliklerin entropisinin, olay ufku alanının, 1/4 ile orantılı olduğunu göstermiştir.
$$S_{BH} = \frac{kA}{4l_p^2} \quad\quad\text{(d.8)}$$
Bu bağıntıya Bekenstein-Hawking bağıntısı denir (9). Burada k Boltzmann sabiti, lp de Planck mesafesidir. Hawking ayrıca, karadeliklerin bir çeşit ışıma yaparak (Hawking ışıması), sonlu bir süre sonra tamamen buharlaşacağını göstermiştir (10, 11). Buna Hawking ışıması adı verilmektedir. Ancak buradaki sorun, Hawking ışımasının özelliklerinin hiçbir şekilde, karadeliğin içine düşen maddelerin özelliklerine dayanmaması, aynı kütle, elektrik yükü ve rotasyona sahip olan karadeliklerin, birbirlerinden ayırt edilmeyeceklerini gösterdi. Yani, başka bir deyişle, karadelik içine düşen cisimlere ait enformasyon yok oluyordu. Bu da karadeliklerde, evrenin toplam entropisinin düştüğü anlamına geliyordu. Yani, Hawking, kuantum teorisinin temellerinden yola çıkarak, sonuç olarak, kuatum teorisinin yine temel taşlarından biri olan “enformasyonun yok edilemeyeceği” ilkesi ile çelişen bir sonuç elde etmişti (12).
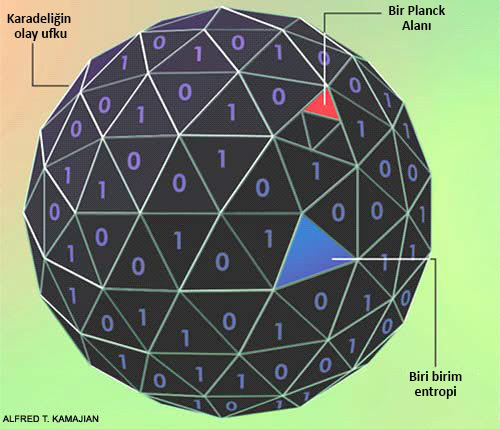
Hawking-Bekenstein Bağıntısı, karadelik yüzeyindeki enformasyonun yalnızca üst sınırını verir
Kuantum Alanları Teorisi’ne (KAT) ait denklemler, zamanın akış yönünden bağımsızdır; yani başka bir deyişle “tersinebilir”dir. Bir sistemin herhangi bir andaki durumu, KAT’a ait denklemler geriye doğru işletilerek, başlangıçtaki farklarına ulaşılabilir. Yani, eğer iki sistem, başlangıçta farklı ise, farklı kalır denebilir. Dolayısı ile sistemi oluşturan ögelere ait enformasyonun hiçbir zaman kaybedilmemesi gerekir. Bu durum, Termodinamiğin 2. Kanunu ile çelişmez. Örneğin, makro düzeyde, bir cisim yandığı zaman ortaya ısıl enerji, çeşitli gazlar çıkar ve geriye cismin külleri kalır. Ancak kuantum ölçeğinde, cisme ait atomlar ve elementer parçacıkların hiçbiri yok olmamıştır ve takip edilemeyecek kadar fazla enformasyon olsa dahi, bu enformasyon vardır ve yok olmamıştır (13).
Dolayısı ile, karadeliklerde yok oluyor gibi görünen enformasyon, fizik teorilerinin ilkeleri arasında bir çelişkiye, yani paradoksa neden olmaktadır (6) ve bu paradoksun bir çözüme ulaştırılması gerekmektedir. Burada, birleştirici olan ilke, Sicim Teorileri’nden (sicimleri temel olarak alan teoriler, birden fazla sayıdadır ve farklı öngörüleri vardır.) gelmektedir ve Holografik ilke olarak isimlendirilir (14).
Bu nokta, bilimdeki halihazırda gözlem veya deneyle şüpheye yer bırakmadan kanıtlanmış olmadığı için, kavramların da birbirleri yerine kullanıldığı ve dolayısı ile akıl karışıklığı yaratan noktalardandır, bu nedenle de biraz üzerinde durmakta fayda var. Sözgelimi, Sicim Teorileri, Genel Görelilik veya KAT kadar sağlam bir şekilde kanıtlanmış bir teoriler değildir; örneğin öngörüleri içerisinde 4 boyuttan fazla boyut olduğu bulunmaktadır ancak buna ait bir gözlem henüz yapılmamıştır. Ayrıca, büyüklükleri Planck mesafesi mertebesinde olduğu düşünülen sicimlerin (10-33m, yani elektrondan 1.000.000.000.000.000 kat daha küçük) kendileri, halihazırda var olan teknoloji ile gözlemlenebilenden çok daha küçüktür. Bu gibi nedenlerle de birçok bilim insanı tarafından şu an için “şık bir matematiksel model” olarak görülmektedir.
Ancak benzer şekilde var olan kütleçekim teorileri, kuantum ölçeğinde; kuantum teorileri de kütleçekim konusunda doğru olmayan sonuçlar vermektedir. Sicim Teorileri, bu ikisinin birleştirilmesi için gösterilen çabanın bir sonucudur.
Holografik ilke ise, kendi başına bir teori olmayıp, Sicim Teorileri çerçevesinde, kuantum ve görelilik teorilerinin birleştirilebileceği noktalardan biridir ve bu anlamda “her şeyin teorisi”ne doğru atılmış önemli bir adımdır. Bu nedenle, kavramsal olarak nerede durduğunu anlamak, hızla yanlış sonuçlar çıkarmamak için önemlidir. Peki ama Holografik ilke, bu iki teori arasında nasıl bir bağ kurmaktadır?
Einstein’ın Görelilik teorilerine göre, içinde bulunduğumuz evren, kendisinden önceki Newton döneminde olduğu gibi, 3 boyutlu bir Öklid uzayı ve sonsuzdan gelip sonsuza giden bir zaman şeklinde değildir. Einstein evreni, uzay-zaman adı verilen, 4 boyutlu sürekli bir ortamdır ve kütleler, bu uzayzaman eğrisinde bükülmelere neden olmaktadır. Yani, kütleçekimi Newton’un denklemlerinde tarif edildiği şekilde uzaktan etkiyen bir kuvvet değil, uzayzamandaki eğrilikten kaynaklanır. Einstein denklemleri, denklemlerdeki “kozmolojik sabit”in sabit eğrilik değerlerinde göre sırasıyla pozitif, sıfır ve negatif değerler ile çözüldüğünde, uzayzamanın şekline göre “de Sitter”, “Minkowski” ve “Anti-de Sitter” uzayı şeklinde isimlendirilir (15).
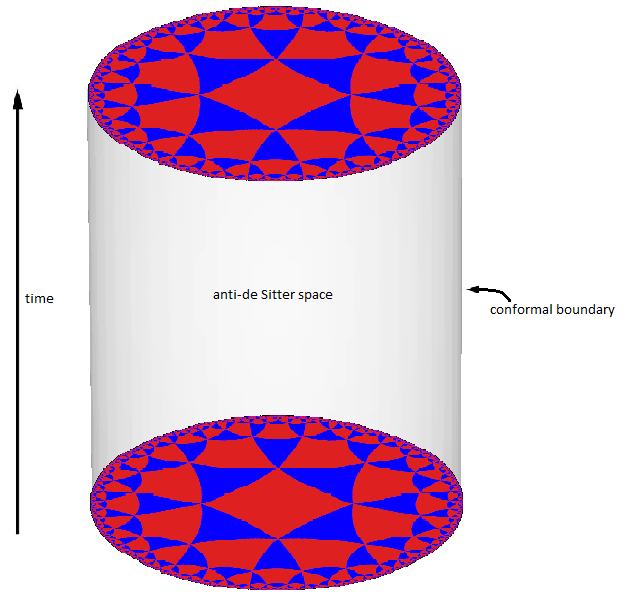
Bazı şartlar altında Anti-de Sitter uzayı, sınırda Minkowski uzayı gibi ele alınabilir (görsel: Wikipedia)
İçinde bulunduğumuz evrenin eğriliği doğrudan ölçüldüğünde, değeri sıfır çıkmaktadır. Yani, bu ölçüm “Minkowski Uzayı”na karşılık gelir. Ancak, Sicim Teorisi çerçevesinde, 3 boyutlu Anti-de Sitter uzayı, sınırında, 2 boyutlu Minkowski Uzayına karşılık geldiği, Leonard Susskind tarafından gösterilmiştir. Buna AdS/CFT Uyuşması [İng. Ads/CFT Correnpondence] denir. Yani, AdS’nin sınırı ile Minkowski uzayı, bu anlamda, aynı olayın iki farklı anlatımıdır denebilir. Bu birinin “yanılsama”, diğerinin “gerçek” durum olduğu anlamına, dolayısı ile de “Matrix’de yaşadığımız” anlamına gelmez. Yalnızca, hologramlarda olduğu gibi, üç boyutlu bir resmin, doğru şekilde oluşturulmuş, iki boyutlu bir yüzey ile gösterildiği durum ile benzerlik gösterdiği anlamına gelir.
Ancak bilim insanları ve bizler gibi bilimi dışarıdan takip eden kişiler, heyecanlanmakta elbette haklıdır. Çünkü, Newton’un kütleçekiminin, genel görelilikteki uzayzaman eğriliği nedeniyle kendiliğinden ortaya çıkması gibi, 3 boyutlu uzay, 2 boyuttaki farklı bir tasvirden ortaya çıkmaktadır. Yani, Sicim Teorisi çerçevesi sayesinde, fiziksel evrene ait özelliklerden biri, daha temel ögeler ile açıklanmaya doğru gitmektedir. Bu durum, bir vadede, bilimde yeni bir paradigma değişimine neden olabilir ve dahası, kuantum teorileri ile kütleçekimin birleştirilmesi yönünde atılmış önemli bir adımdır. Bugün keşfedilecek bir kuatum-kütleçekim teorisi, şüphesiz yüz yıldan uzun süredir, en büyük ve heyecan verici gelişme olacaktır.
Ancak şunu da belirtmekte fayda var, Holografik İlke, içinde bulunduğumuz evrende olduğu gibi, değişken sınırları olan ve karadeliklerden hiçbir cismin kaçamamasının aksine, sınırdan giriş-çıkışın gerçekleştiği durumları ve 3 boyuttaki nedenselliği açıklamıyor. Bu nedenle, her ne kadar, içinde bulunduğumuz evren de, kendi ışığın ve nedenselliğin ulaşabileceği uzaklık anlamında, bir karadelikte olduğu gibi, bir çeşit olay ufkuna sahipse de, holografik ilkenin henüz bu tür durumları da açıklayabilecek şekilde genişletilmesi gerekiyor.
Maalesef, ajan Smith’i eşek sudan gelene kadar pataklamak için bir süre daha beklememiz gerekiyor.
Kaynaklar:
(1) https://en.wikipedia.org/wiki/General_relativity
(2) https://en.wikipedia.org/wiki/Black_hole
(3) http://hepweb.ucsd.edu/ph110b/110b_notes/node75.html
(4) https://en.wikipedia.org/wiki/Schwarzschild_metric
(5) http://www.zweigmedia.com/diff_geom/Sec15.html
(6) https://www.youtube.com/watch?v=yMRYZMv0jRE
(7) https://en.wikipedia.org/wiki/Jacob_Bekenstein
(8) https://en.wikipedia.org/wiki/Compton_wavelength
(9) https://en.wikipedia.org/wiki/Black_hole_thermodynamics
(10) Particle Creation by Black Holes, Hawking, S W, 1975, Commun. math. Phys. 43, sayfa 199—220
(11) https://en.wikipedia.org/wiki/Hawking_radiation
(12) Black Holes and Baby Universes, Hawking, SW, 1993, Bantam Books, sayfa 95
(13) https://en.wikipedia.org/wiki/Quantum_no-deleting_theorem
(14) https://en.wikipedia.org/wiki/Holographic_principle
(15) https://en.wikipedia.org/wiki/Anti-de_Sitter_space