Zamanın Gerçekliği Hakkında Bir Savunma

Tim Maudlin, bir çok bilim insanının aksine, gündelik zaman algımızın, bize anlatıldığı kadar yanlış olmadığı fikrini savunuyor.

Fizikçiler ve filzoflara, bizlere dünya hakkında bildiğimiz her şeyin yanlış olduğunu söylemekten daha fazla keyif veren bir şey yok gibi görünüyor. Sağduyuyu, saçmalık şeklinde açığa vurmaktan özel bir haz alıyor gibiler. Ancak Tim Maudlin, dünya hakkındaki doğrudan izlenimlerimizin, bize anlatılandan çok daha iyi bir rehber olduğu görüşünde.

Bunun her koşulda doğru olduğunu savunuyor da değil. New York Üniversitesinde Profesör olarak görev yapan ve dünyanın önde gelen fizik felsefecilerinden olan Maudlin, ismini “dolanık” kuantum parçacıklarının tuhaf davranışları konusundaki çalışmaları ile duyurdu. Alabildiğine mantık dışı davranışlar gösteren kuantum dolanıklığı konusunda, örneğin, dolanıklığının yaratabileceği farkın olması gerekenden daha az önemsendiğini düşünüyor. Diğer taraftan, fizikçilerin, özellikle zamanın doğası konusunda, bizlere ait geleneksel görüşlerin yanlış olduğunu iddia etmekte çok aceleci davrandığı kanısında.

Maudlin, alışıldık ve demode bir zaman görüşüne sahip. Zamanın, kendisine içkin bir yönü var. Zaman, daha derin bir gerçeklikten ortaya çıkmıyor, kendisi temel. Değişim, bir yanılsama veya bakış açısından kaynaklanan yapay bir yaratımdan ziyade, gerçek. Fizik yasaları, her anı yaratacak şekilde, zaman içerisinde hareket ediyor. Maudlin, matematik, fizik ve felsefeyi bir araya getirerek, bilim insanlarının ve filozofların bu yaygın düşünceleri reddetmek için sıkça öne sürdükleri nedenleri yıkmaya çalışıyor.

Şu anki çalışmasının (ilk cildi 2014 yılında yayımlanan, Fiziksel Geometri için Yeni Temeller’in [New Foundations for Physical Geometry ] ikinci cildi) hedefinde ise matematiksel argümanlar bulunuyor. Maudlin’e göre, modern fizik, zamanı, özünde uzay ile aynı şekilde kavramsallaştırıyor. Uzay’ın, bizlerin genel olarak anladığı şeklinde, kendisine içkin bir yönü bulunmuyor – yani eşyönlü. Mekânsal sezgilerimizi zamana uyguladığımızda, ister istemez zamanın da kendisine içkin bir yönü olmadığını varsayıyoruz. Yeni Temeller , topolojiyi, zaman ve uzay arasındaki farkı daha açık bir şekilde anlatabilecek şekilde yeniden kurguluyor. Geleneksel olarak, topoloji – geometrik yapıların ilk seviyesi – bir noktanın uzay veya zamandaki komşuluğunu tarif etmek için açık kümeler kullanılarak tanımlanır. “Açık”, keskin kenarı olmayan bir bölge anlamına gelir; kümedeki her nokta, aynı kümedeki başka noktalar ile çevrilidir.

Maudlin, bunun yerine topolojiyi doğrular üzerine kurmayı öneriyor. Bunun gündelik geometrik sezgilerimize daha yakın olduğunu düşünüyor. Ve bu şekilde, standart topolojinin sonuçlarına ulaşabilmek için, doğruların yönü olması gerektiği sonucuna ulaşıyor, tıpkı zamanın yönü olduğu gibi. Maudlin’in yaklaşımı, standart topolojiyi, doğrultusu olan geometrileri içerecek şekilde genişleten yaklaşımlardan ayrılıyor; buradaki bir genişletme değil, doğrultuyu temelden dahil eden yeni bir kurgu.

Buradaki röportaj, Mart ayında Quanta Magazine’de yayımlanan yazısnın kısaltılmış ve yeniden düzenlemiş bir halidir.

 

Biri neden zamanın bir doğrultusu olduğunu düşünür? Bu fizikçilerin sıkça söylediklerine aykırı gibi görünüyor.

Bence [bu soru] biraz tersten. Sıradan birine gidip, zamanın doğrultusu olup olmadığını, geleceğin geçmişten farklı olup olmadığını ve zamanın geleceğe doğru ilerleyip ilerlemediğini sorun. Doğal görüş budur. Daha ilginç olan ise, nasıl olup da fizikçilerin kendilerini zamanın bir doğrultusu olmadığına ikna edebilmiş olmalarıdır.

 

[Bilim insanları] Bunun, zamanı dördüncü bir boyut olarak alan Einstein’ın özel görelilik teorisinin bir sonucu olduğu şeklinde yanıt vereceklerdir.

Zamanın yalnızca bir dördüncü boyut olduğu düşüncesi son derece yanıltıcı bir düşünce. Özel görelilikte, zaman doğrultuları, uzay doğrultularından yapısal olarak farklıdır. Zaman-benzeri doğrultularda, gelecek ve geçmiş için fazladan ayrımlar ortaya çıkar, diğer taraftan herhangi uzay-benzeri doğrultuda, sürekli bir şekilde başka bir uzay-benzeri doğrultuya doğru dönebilirim Zaman-benzeri doğrultuların iki sınıfı sürekli bir şekilde birbirine dönüştürülemez.

Standart geometri uzay-zamanı incelemek için geliştirilmemiştir. Yalnızca uzay incelemeleri amacıyla geliştirilmiştir, ve uzayların kendilerine ait bir yönlülükleri bulunmaz. Ve sonra bir amaç için geliştirdiğiniz bu aracı alıp, başka bir amaçla kullanmaya çalışıyorsunuz.

 

Görelilik 20. yüzyılın erken dönemlerinde geliştirildiğinde, insanlar bu sorunu fark etmeye başlamışlar mıydı?

Bunu bir sorun olarak görmüş olduklarını sanmıyorum. Yapılan geliştirme son derece cebirseldi, ve bir teknik ne kadar cebirselse, yapmakta olduğunu şeyle ilgili geometrik sezgilerden o kadar uzaklaşırsınız. Yani, diyelim ki standart bir uzay-zaman metriği hesabı geliştirdiniz, sonrasında da “Peki buna negatif sayılar yerleştirirsem ne olur?” diye soruyorsunuz. Bu soru cebirsel olarak gayet makuldür. Geometrik olarak ise ne anlama geldiği o kadar da açık değildir. Ve insanlar şimdi de “Peki, ya zamanın iki boyutu olsaydı ne olurdu?” diye sorarak aynı şeyi yapıyorlar. Tamamen cebirsel bir soru olarak bunu sorabilirim. Ancak bana, fiziksel olarak, zamanın iki boyutu olmasının ne anlama geldiğini sorarsanız, en ufak bir fikrim yok. [Zamanın] İki boyutlu bir şey olması, zamanın doğası ile tutarlı mı? Çünkü eğer zamanın yaptığı şeyin, olayları sıralamak olduğunu düşünüyorsanız, bu durumda bu sıra, doğrusal bir sıradır, ve siz de temelde tek-boyutlu bir düzenleme şeklinden bahsediyorsunuzdur.

 

Ve siz bu nedenle zamanın doğrusallığına izin verebilmek için geometriyi yeniden kurguluyorsunuz. Bu nasıl işliyor?

Ben aslında fizikten yola çıkmadım. Yalnızca topolojiyi anlamaya çalışarak başladım. [Bir şeyler] öğrettiğiniz zaman, kendi cehaletiniz ile yüzleşmeye zorlanıyorsunuz. Bir sınıfa uzay ve zaman hakkında ders verirken, bazı öğrencilere standart topolojiyi açıklamaya çalışıyordum, ve kendimin de anlamadığını fark ettim. Kullanıyor olduğum teknik araçlar ile fikirler arasındaki bağlantıyı göremiyordum.

Size bir torba dolusu nokta verdiğimi düşünün. Bir şekli yok. Bu nedenle, bunlara geometrik olarak tanımlanabilir olmaları için bir yapı sağlamalıyım. Standart yaklaşımda, hangi nokta kümelerinin açık kümeler olduğunu belirtirim. Kendi yaklaşımımda ise, hangi nokta kümelerinin doğrular olduklarını belirtiyorum.

 

Bu lisede öğretilen sıradan geometriden ne şekilde farklılaşıyor?

Doğrular üzerine kurulu bu yaklaşımda, doğrulara yönler vermek gayet doğal bir şey. Aksiyomlar seviyesinde uygulamak kolay. Eğer Öklid geometrisi kullanıyorsanız, bu aklınıza gelmez, çünkü aklınızdaki Öklid geometrisinde, A’dan B’ye sürekli bir doğru var ise, bu aynı zamanda B’den A’ya da sürekli bir eğridir – Öklid doğrularında bir doğrultu bulunmaz.

 

Tamamen matematiksel bir bakış açısından bakarsak, sizin yaklaşımınız neden tercih sebebi olabilir?

Benim yaklaşımımda, bir noktalar kümesine doğrusal bir yapı veriyorsunuz. Eğer doğruları benim aksiyomlarıma uygun bir şekilde yapılandırırsanız, açık küme için doğal bir tanım ortaya çıkıyor ve bu da bir topoloji yaratıyor.

Bir diğer önemli kavramsal avantaj ise, bir doğruyu ayrık olarak düşünme konusunda hiçbir sorun olmaması. İnsanlar yalnızca sonlu sayıda kişinin olduğu şekilde sıralar/doğrular oluşturabilir, ve sıradaki bir sonraki kişinin kim olduğu ve onun arkasındaki kişinin kim olduğu gibi şeylerden bahsedebilirsiniz. Bir doğru (sıra) fikri, kendisinin ayrık veya sürekli olması konusunda tarafsızdır. Böylece elinize bu genel yaklaşım geçmiş oluyor.

 

Bu tür bir modifikasyon fizik için neden önemli?

Uzay-zaman hakkında konuşmaya başladığımız anda, zamanın bir doğrultusu olduğu fikri açıkçası başlangıç noktalarımızdan biridir. Geçmiş ve gelecek arasında büyük bir fark var. Ve bu nedenle uzay-zaman hakkında, yani zamansal özellikleri olan bir şey hakkında fikir yürütmeye başladığınızda, [akla gelen] doğal bir düşünce, kendisine içkin olarak doğrultusu bulunan bir şey hakkında fikir yürütüyor olduğunuzdur. Ve eğer geometrik nesnelerin doğrultuları olabilirse, onları bu fiziksel doğrultuyu temsil etmeleri için kullanabilirsiniz.

 

Fizikçilerin zamanın neden bir yönü olmadığına dair başka argümanları mevcut.

Çoğu zaman [fizik] kanunlarında zaman-tersinimi simetrisi olduğunu işitirsiniz. Fakat zaman-tersinimi simetrisini sıradan bir şekilde tarif etmek, zamanın bir doğrultusu olduğunu önceden varsayar. Şöyle şeyler söylenebilir: “Newton fiziğine göre, eğer bir bardak masadan düşüp, yere çarpıp kırılabiliyorsa, yerdeki kırıkların, yerin çabası ile itilip, bardak olarak tekrar bir araya gelip, masaya geri sıçraması da fiziksel olarak mümkündür.” Bu doğru. Fakat şuna dikkat edin, bu anlatımların her biri zamanın bir doğrultusu olduğunu önceden varsayıyor. Şöyle ki, bardağın düşmesi ve bardağın sıçraması arasında bir fark olduğu önceden varsayılıyor, ayrıca bardağın kırılması ve bardağın bir araya gelmesi arasında da bir fark var. Ve bu ikisi arasındaki fark, her zaman hangi yönün gelecek, hangi yönün geçmiş olduğudur.

Bu zaman-tersiniminin olduğunu kesinlikle reddetmiyorum. Ancak zaman-tersinimi, zamanın bir yönü olmadığına işaret etmiyor. Yalnızca, fizik kanunlarının izin verdiği her olay için, bunlarla bağlantılı başka olaylarda, çeşitli şeylerin, örneğin hızların ve benzer şeylerin tersine dönmüş olduğunu belirtiyor. Ancak her iki durumda da bunları zamanda ileri gitmesine izin verilen süreçler gibi ele alıyorsunuz.
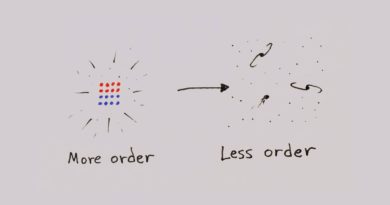
Bu şu soruyu doğuruyor: Neden bunlardan birini sıkça görürken, diğerini görmüyoruz? Bu soru termodinamik, entropi ve benzerleri ile ilgili.

 

Eğer zamanın bir doğrultusu varsa, termodinamik zaman oku yine de bir sorun teşkil ediyor mu?

Buradaki sorun [zamanın] oku ile ilgili değil. Sorun neden her şeyin bir düşük-entropi durumu ile başlamış olduğunu anlamakta. Düşük-entropi durumuyla olan başlangıca sahip olduktan sonra, sıradan termodinamik argümanlar sizi mümkün olan başlangıç koşullarının çoğunun yükselen bir entropiye neden olacağını düşünmeye sevk ediyor. Bu yüzden asıl soru, neden her şey bu kadar düşük bir entropi ile başladı?

Seçeneklerden biri, evrenin zaman içerisinde sonlu olduğu ve bir başlangıç durumu olduğu, ama o zaman da şu soru ortaya çıkıyor: “Başlangıç koşulunun neden düşük olduğunu açıklayabilir misiniz?”, ki bu soru, “Herhangi bir başlangıç koşulunu açıklayabilir misiniz?” sorusunun bir alt sorusudur. Herhangi bir şeyden kaynaklanmadıysa, daha en baştan bunu açıklamak ne anlama gelmektedir?

Diğer bir olasılık ise büyük patlamadan önce bir şeylerin var olduğudur. Eğer büyük patlamanın, evrenin bir tür ön-evrenin şişmesi ile veya kaotik olarak genişleyen bir uzay-zamanın şişmesi oluştuğunu düşünüyorsanız, bu şişmenin de bir fiziği olacaktır ve bu şişmenin fiziğinin belli karakterdeki kabarcıklara işaret etmesini umarsınız.

 

Başlangıçtaki düşük-entropi durumu hakkında bir açıklamaya ulaşmamız gerektiği göz önünde bulundurulduğu takdirde, neden zamana ait içsel bir yönlenmeye ihtiyaç duyuyoruz? Eğer zamanın bir doğrultusu yoksa, düşük-entropili bir durumun belirlenmesi etkin bir yön belirlenmesi için yeterli olmaz mı?

Eğer zamanın bir doğrultusu olmasaydı, bana öyle geliyor ki, bu onu yalnızca bir diğer uzaysal boyut haline getirirdi, ve eğer elimizde yalnızca uzaysal boyutlar varsa, bence evrenden hiçbir şey olmuyordur. Dört boyutlu uzaysal bir nesne düşünebilirim, fakat bu nesnede hiçbir şey gerçekleşmez. Bu insanların sıklıkla sabit veya rijit veya değişmeyen veya buna benzer bir, tırmak içinde, “blok evren”i açıklama şekilleri, çünkü evreni dört boyutlu uzaysal bir nesne olarak ele alıyorlar. Eğer elinizde bu varsa, ne tür bir başlangıç koşulunun – veya sınır koşulunun, çünkü artık başlangıçtan bahsedemeyiz – zamanı yaratabileceğini bilemiyorum.

Sınırlardan birinde düşük entropi olduğunu düşünün; buradan yola çıkarak geri kalan her şeyi açıklıyorum. Şunu merak edebilirsiniz: “Peki ama neden bu sınır? Neden her şeyin varsayımsal olarak dengede olduğu diğer sınırdan başlamıyoruz?” Bu sınırdaki ilginç özellikler düşük entropi olması değil – burada yüksek entropi var – bunun yerine, uzun süreli bir entropi düşüşüne götüren, özel bir mikro durum olması. Şimdi ise bana düşük-entropili bir başlangıç durumundan geldiği için ilginç görünüyor. Fakat şimdi “başlangıç” ve “son” kelimelerini kullanıyorum, açıklama için belli neden-sonuçsal ve üretimsel fikirlere başvuruyorum. İlk biçimleri ve son biçimleri birbirinden ayırt edecek, ve bu neden-sonuçsal deyimleri güvence altına alacak bir zaman doğrultunuz yoksa, bu açıklamaların nasıl yapılabileceğinden pek de emin değilim.

Fakat tüm bunlar öyle görünüyor ki – ne diyebilirim? Fiziksel dünyadan çok uzak görünüyorlar. Burada oturuyoruz ve zaman ilerliyor, ve zamanın ilerliyor olmasının ne anlama geldiğini biliyoruz. Zaman aslında geçmiyor demenin veya yalnızca artan entropi nedenliyle ortaya çıkıyor demenin ne demek olduğunu bilmiyorum.

 

Blok evrenden pek de hoşlanıyor gibi değilsiniz.

Blok evren anlayışının inandığım bir yönü var. Geçmişin, şimdi kadar gerçek olduğunu ve bunun da gelecek kadar gerçek olduğunu düşünüyorum. Geçmişte gerçekleşen şeyler gerçekti. Acılar gerçek acılardı, ve gelecekte de gerçek olacaklar; ve bir tek geçmiş ve bir tek gelecek var. Eğer tüm bunlar blok evrene inanmak anlamına geliyorsa, tamam.

İnsanlar sıkça, “Görelilik nedeniyle blok evrene inanmak zorunda kaldım,” diyorlar. Blok evren, tekrar etmek gerekirse, rijit bir tür yapı. Katı fiziksel gerçekliğin bütünü, dört boyutlu yapıyı ve içerisinde neler olduğunu tarif ediyor. Newton mekaniğinde bu nesnede mutlak eş-zamanlılık katmanları mevcuttur. Görelilikte bu yoktur; bunun yerine bir ışık-konisi yapınız vardır. Yani farklı bir geometrik karakteri vardır. Ancak bu farklı geometrik karakterin, zamandan veya zamansallıktan kurtulmamızı nasıl sağladığını göremiyorum.

Blok evrenin statik olması fikri beni rahatsız ediyor. Bir şeyin statik olduğunu söylemek ne demektir? Zaman geçerken, değişmediğini söylemektir. Fakat blok evren zamanın içerisinde değil, zaman onun içerisinde. Statik olduğunu söylediğiniz zaman, bu bir şekilde değişim olmadığı anlamı gelir, hiçbir şey aslında değişmez, değişim bir yanılsamadır. İnsanın aklını karıştırıyor. Fizik dünya hakkında gerçekten tuhaf şeyler ortaya çıkarmıştır, ancak değişimin bir yanılsama olduğunu değil.

 

Zamanın geçmesi demek ne demektir? “Zamanın bir doğrultusu olması” ile eş anlamlı mıdır, yoksa ek olarak bir şey var mı?

Ek olarak bir şey var. Zamanın geçmesi demek, olayların doğrusal bir şekilde, daha önce ve daha sonrakiler şeklinde sıralı olması anlamına gelir. Dünyanın nedensel yapısı, zamansal yapısına bağlıdır. Evrenin şimdiki durumu, daha sonra gelen durumlarını yaratır. Sonraki durumları anlamak için, önceki durumlara bakarsınız ve tersini yapmazsınız. Elbette, sonraki durumlar, daha önceki durumlar hakkında pek çok bilgi sağlarlar ve sonraki durumlar ve fizik kanunları ile, önceki durumları çıkarsayabilirsiniz. Fakat, sonraki durumların, önceki durumları açıkladığını söylemezsiniz. Nedenselliğin yönü, aynı zamanda açıklamanın yönüdür.

 

Burada bir yaratım veya üretim olduğunu doğru mu anlıyorum – bir makinanın işlemesi, bir anın diğerini ortaya çıkarması ve bir diğerini ortaya çıkarması?

Evet, bu kesinlikle çizdiğim resmin önemli bir parçası. Bu makina, tam olarak doğa kanunları. Bu, doğa kanunlarına bir kısıtlama veriyor – yani, [doğa kanunlarının] zamansal evrim kanunları olmaları gerekiyor. Bunlar, zaman geçtikçe, yeni durumların nasıl eski durumların yerini aldığını açıklayacak kanunlar olmalılar. [Buradaki] İddia, yalnızca zamansal olan temel kanunların olmaması ve uzaysal düzenlemelerin bulunduğu her durumda, zamansal açıklamalarının olduğudur.

 

Bu sizi bir kanunun dahi ne olduğuna ait farklı bir görüşe vardırıyor mu?

Beni çoğunluğun görüşünden farklı bir görüşe götürüyor. Ben kanunların bir çeşit ilkel metafiziksel bir durumları olduğunu, kanunların başka şeylerden türetilmediğini düşünüyorum. Daha ziyade, tam tersi: Diğer şeyler işlemekte olan kanunlar ile türetiliyor, üretiliyor ve açıklanıyor. Bu burada, “işlemek” kelimesi zamansal bir karakteristik içeriyor.

 

Sizinki neden bir azınlık görüşü? Çünkü bana öyle görünüyor ki, dışarıdaki pek çok insana fizik kanunlarının ne işe yaradığını sorsanız, “Bunlar bir makinanın parçaları,” derler.

Benim felsefi görüşlerimin sık sık sadece bir fizik veya bir kozmoloji dersi aldığınızda söylenen her şeyi ciddiye alırsanız sahip olacağınız naif görüşler olduğu söylerim. Bir Newton mekaniği sınıfında, bazı kanunları yazacak ve “işte bunlar Newton mekaniği kanunlarıdır,” diyeceklerdir. Bunlar gerçekten de başlayacağınız temel bilgilerdir.

Tuhaf fikirlerim olduğunu düşünmüyorum. “Zaman geçmiyor,” veya “zamanın geçişi bir yanılsamadır” görüşlerinin oldukça tuhaf olduğunu düşünüyorum. Yanlış olması gerektiğini söylemiyorum, ancak bu şekilde düşünüyor olmadığınız için dikkat çekmesi gerektiğini söylüyorum.

 

Tüm bunlar zamanın temel veya [daha temel nedenlerden] ortaya çıkan bir şey olması hakkında ne anlama geliyor?

Zamanın ortaya çıkmasının, gerçek anlamda ne anlama geldiğini hiçbir zaman tam olarak ne anlama gelmesi gerektiğini anlayamadım. Kanunlar genel olarak zamansal diferansiyel denklemler. Şeylerin nasıl evrimleştiğini anlatıyorlar. Yani, eğer zaman yoksa, hiçbir şey evrimleşemez. Zamansal ortaya çıkış nedir ve nasıl anlaşılabilir? Bu şunun gibi, evrenin belli evrelerinde zaman yoktur; sonra başka evrelerinde ise zaman vardır, burada zamanın, zamansızlıktan zaman içerisinde ortaya çıkması gibi bir şey var ve bu nedenle tutarsız görünüyor.

Analiz etmeyi hangi noktada bırakmanız gerek? Nerede durmalısınız – Wittgenstein’ın söylediği gibi, küreğiniz nerede eğriliyor [Felsefi Araştırmalar – Madde 217]? Benim için, zamansallık fikri veya zaman, evrenin, başka şeylerle açıklanamayan temel bir özelliğine ulaştığımı düşündüğüm bir nokta.

 

Bu yazının orijinali Quanta Magazine‘de yayımlanmıştır. Orijinal yazıya buradan ulaşabilirsiniz.