‘Kıyamet Günü Argümanı’ nedir ve insanlık ne zaman yok olacak? (J. Richard Gott III)
Hiç insan ırkının soyunun ne zaman tükeneceğini merak ettiğiniz mi? Cevabınız evetse, Kıyamet günü argümanı bunun için bir yaklaşım sunuyor…
Kıyamet günü argümanı [İng. Doomsday argument] özetle, Kopernikçi gökbilim devriminin arkasına yatan Kopernik ilkesi veya diğer adıyla sıradanlık ilkesinin, insan türünün gelecekteki üyelerinin sayısı konusunda bir yaklaşım geliştirmek için uygulamış halidir denebilir. Kopernik, Yeryüzünün Evrenin merkezi olması üzerine kurulu Batlamyucçu yaklaşım ile ortaya konan gökcisimlere ait hareketlerin karmaşıklığının, hareketin merkezinde Yeryüzünün değil, Güneşin olduğu bir model ile daha sade bir hale gelebileceğini fark etmişti.
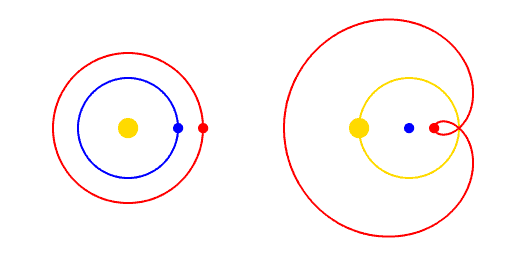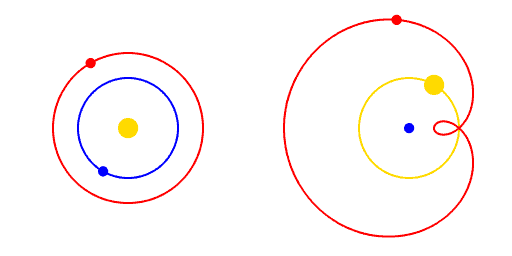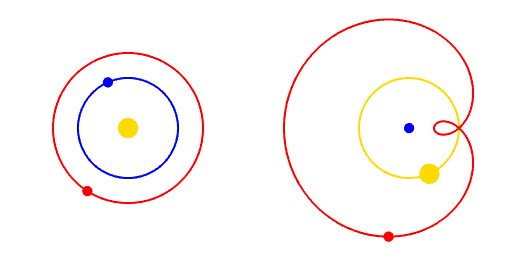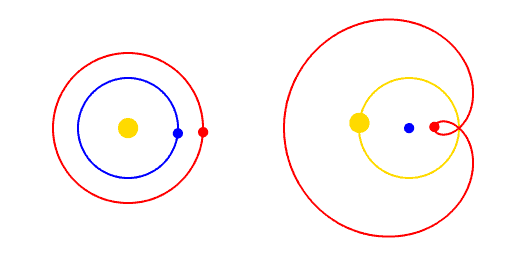
Fakat bunun için bir varsayım yapılması gerekiyordu: Dünya Evrenin merkezinde değil, diğer gezegenlerle beraber, Güneşin çevresinde dönmektedir. Yani Yeryüzünün konumu ayrıcalıklı değildir; diğer gezegenler arasında, sıradan bir konumu vardır. İşte bu ilke, bilimde önemli bir yer kaplar; çünkü sözgelimi her gözlemin özel bir durumu olduğunu varsaymak, her deneyin sonuçlarının birbirinden farklı olacağını varsaymak, bilimsel bilginin birikimini önleyecektir.
Peki, bu ilke insanlık için ne söylemektedir? Evrendeki konumumuz ayrıcalıklı olmadığına göre, bir tür olarak ayrıcalıklı olabilir miyiz? Darwinci devrim, olmadığımızı göstermiştir. Canlılık, insanlığın tekelindeki bir şey değil, milyonlarca yıl önce başlamış ve süregitmekte olan bir süreçtir; herhangi bir olayın, kaçınılmaz olarak yalnızca bizim ortaya çıkmamız için ilerlemiş olduğunu düşünmek için bir neden bulunmuyor. Daha sonraki Freudçu devrim ise, insanlığın bir üyesi olarak dahi bir ayrıcalığımız olmadığını, kişisel gibi görünen her şeyin türün her bireyinde bulunan aynı zihinsel süreçlerin dışavurumları olduğunu göstermiştir.
İşte, Kıyamet günü argümanı bunu anlatır. Bizim birey olarak insan türündeki konumumuz ayrıcalıklı olamaz; dahası, sıradan olmalıdır. Yani, var olduğu andan itibaren insan türünün üyeleri arasında, %95 ihtimalle, %95’inin içinde bulunuyoruz. Bu yargı, kendi başına totolojiktir, ancak açılımları yine de bazı bilgiler verir. Örneğin, çıkan sonuçlardan biri, kendisiyle ilgili rastgele bir anda gözlem yapılan bir gözlemlenebilirin (yani hakkında gözlem yapılabilen herhangi bir şey) geçmişte ne kadar uzun süre var olduysa, gelecekteki varlığının da muhtemelen o kadar uzun olacağına işaret eder. Bu rahatlatıcı bir şey olarak görülebilir, fakat aynı zamanda buna bir sınır da koyar ve sonsuzluğu elimizden alır.
Kıyamet günü argümanı, ilk kez Brandon Carter tarafından 1983 yılında ortaya konmuştur, bu nedenle Carter Felaketi olarak da isimlendirilir. Daha sonra bağımsız olarak Holger Bech Nielsen ve J. Richard Gott III tarafından ilerletilmiştir. Buradaki makale, Gott’a ait 1993 tarihli yazıdır. İyi okumalar dileriz.
İtalikler, kalın karakterler ve [köşeli parantezler] yazara, {küme parantezleri} çevirene aittir.
-oo-
KOPERNİK İLKESİNİN GELECEKTEN BEKLENTİLERİMİZ İLE İLGİLİ İMALARI
Yazan: J. Richard Gott III
Orijinal adı: Implications of the Copernican principle for our future prospects, 1993
Özet. Yalnızca rastgele zeki bir gözlemci olduğunuz varsayımında bulunmak, türümüze ait yaşam süresini {İng. longevity}, %95 güven seviyesi ile 0.2 ila 8 milyon yıl olarak elde edilmesini sağlar. Daha ileri bir değerlendirme, bizim Galaksiyi kolonileştirmemizin muhtemel olmadığına ve muhtemelen zeki türlerin nüfusuna ait medyan değerden daha yüksek bir nüfusa sahip olacağımıza işaret eder.
KOPERNİK devrimi, bize elimizde yeterli neden olmadan Evrende özel bir yerimiz olduğunu varsaymanın hata olduğunu öğretti. Darwin, köken anlamında, diğer türlerin üzerinde bir ayrıcalığımız olmadığını gösterdi. Sıradan bir süperkümede bulunan sıradan bir galaksideki sıradan bir yıldızın çevresindeki konumumuz, giderek daha az ve daha az özel görünmeye devam ediyor. Uzamsal olarak özel konumda bulunmadığımız fikri, kozmoloji için can alıcı olmuş; kozmik arka plan ışımasının3,4 varlığını ve spektrumunu tahmin etme1,2 konusunda dikkate değer ölçüde başarılı olmuş olan Genel Görelilikteki, homojen ve izotropik Friedmann kozmolojik modellerine doğrudan önayak olmuştur. Kopernik ilkesi, astronomide işe yarar, çünkü zeki gözlemcilerin bulunabileceği onca yer arasında, tanım gereği yalnızca az sayıda özel olan yer ve birçok özel-olmayan yer vardır; bu yüzden özel olmayan bir yerde bulunma olasılığınız daha fazladır. Bu fikir, bizim türümüze ait olan da dahil olmak üzere, çeşitli gözlemlenebilirlerin {İng. observables} gelecekteki yaşam süresi konusunda tahminde bulunulmasını sağlar. Bunun, uzak gelecek, Dünya dışı zekâ araştırmaları (SETI) ve uzay yolculuğu konusundaki sonuçlarını tartışacağım.
Delta t argümanı
Kendisine ait ölçüm yapabildiğimiz her şeyin yalnızca \({{t}_{başlangıç}}\) ve \({{t}_{son}}\) anları arasında kalan zaman aralığında gözlemlenebileceğini varsayarsak ve ‘ye ait herhangi bir özel durum mevcut değilse, bu durumda \({{t}_{şimdi}}\)’nin bu aralıkta, rastgele bir noktada bulunmasını bekleriz. \({{t}_{gelecek}}=\left( {{t}_{son}}-{{t}_{şimdi}} \right)={{t}_{geçmiş}}=\left( {{t}_{şimdi}}-{{t}_{başlangıç}} \right)\), tahmini, \({{t}_{gelecek}}\)’i, %50 ihtimalle olduğundan az, %50 ihtimalle de olduğundan fazla verecektir. Eğer, \({{r}_{1}}=\left( {{t}_{şimdi}}-{{t}_{başlangıç}} \right)/\left( {{t}_{son}}-{{t}_{başlangıç}} \right)\), 0 ve 1 arasında düzenli dağılımı olan rastgele bir sayı ise, \(P=0.95\) ile verilen, \({{r}_{1}}\)’in,\(0.025<{{r}_{1}}<0.975\) olduğu bir olasılık mevcuttur; veya eşit bir biçimde aşağıdaki yazılabilir:
\[\begin{gather}
& \frac{1}{39}{{t}_{geçmiş}}<{{t}_{gelecek}}<39{{t}_{geçmiş}} \\
& \text{(%95 Güven seviyesi)} \\
\end{gather}\quad\quad(1)\]
Benzer şekilde, aşağıdaki yazılabilir:
\[\begin{gather}
& \frac{1}{3}{{t}_{geçmiş}}<{{t}_{gelecek}}<3{{t}_{geçmiş}} \\
& \text{(%95 Güven seviyesi)} \\
\end{gather}\quad\quad (2)\]
Denklem (1), bize, bir şeyin geçmişte gözlemlenebilir olduğu sürenin yalnızca geçmişinde geçirdiği felaketlere karşı sağlamlığının bir ölçüsünü değil, aynı zamanda gelecekteki gözlemlenebilirliğini etkileyecek herhangi bir felakete karşı sağlamlığının da kaba bir ölçüsünü verir; çünkü, denklem (1)’in işlemesi için gereken tek şey son tahlilde sadece bir gözlemci olarak sizin konumuzun özel olmamasıdır. Sadece bir örnek olarak, ben, ilk kez 1969 yılında Stonehenge’i (\({{t}_{geçmiş}}\approx 3,868\text{yıl}\)) ve Berlin Duvarını gördüm (\({{t}_{geçmiş}}\approx 8\text{ years}\)). Benim rastgele bir gözlemci olduğumu varsayarsak, \({{t}_{başlangıç}}\) ve \({{t}_{son}}\) arasında rastgele bir konumum olması gerekir (\({{t}_{son}}\), Duvarın yıkılması veya onu gözlemleyecek hiçbir ziyaretçinin kalmaması olaylarından hangisi daha önce gerçekleşirse, odur). Duvar, 20 yıl sonra yıkılmıştır, yani denklem (1)’in %95 güven seviyesi sınırları içerisinde, \({{t}_{gelecek}}=2.5{{t}_{geçmiş}}\) vererek. Delta t argümanını (\(P = 0.95\)) uygulamak, doğru bir şekilde Stonehenge’in, 24 yıl sonra bugün hâlâ gözlemlenebilir olacağını öngörür (çünkü denklem (1)’den \({{t}_{gelecek}}\approx 99\text{yıl}\) elde edilir). 1977 yılında S.S.C.B’yi ziyaret ettim (\({{t}_{geçmiş}}\approx 55\text{yıl}\)). O sıralarda genel olarak gelecekte belirsiz süre boyunca var olacağı varsayılıyor olmasına rağmen, 14 yıl sonra sona erdi (denklem (1)’in sınırları ile tutarlı bir şekilde, \({{t}_{gelecek}}=0.25{{t}_{geçmiş}}\)). Denklem (1)’in, gerçekleştirdiğim ziyaret bir şekilde S.S.C.B’nin yıkılışına neden olduğu için değil; bunun yerine geçmişe dönüp baktığımızda, ziyaretimin zamanlamasının sıra dışı hiçbir özelliği bulunmaması nedeniyle sağlanmış olduğu görülüyor. Nature 123 yıldır yayımlanıyor; delta t argümanı (\(P=0.95\)) gelecekte yayımlanma süresinin 3.15 yıldan fazla, ancak 4,800 yıldan az olacağını öngörüyor.
Gelecekteki ömrümüzün uzunluğu
Carter’ın5 bulgularıyla tutarlı bir şekilde, evrende zeki türlerin halihazırda düzenli bir oranda ortaya çıkmakta olduğunu farz edelim. ‘Zeki’ türler ile, öz-farkındalığı olan, soyut akıl yürütme için gereken bilişsel yeteneğe sahip, gelecek hakkında düşünebilen, sanatsal üretimde bulunabilen v.b. türleri kastediyoruz. Şu ana kadar, biz, homo saphiens, Yeryüzünde bu tanıma uyan6 yegâne türüz. Bu zeki türlerin, bilinmeyen bir nesil tükenme oranı \({{\lambda }_{0}}\)’a tabi olduğunu varsayalım. Bugün hayatta olan \({{N}_{toplam}}\) zeki türün \({{t}_{p}}\) yaş dağılımı şu şekildedir:
\[N\left( {{t}_{p}} \right)\text{d}{{t}_{p}}={{N}_{toplam}}{{\lambda }_{0}}\exp \left( -\lambda {{t}_{p}} \right)\text{d}{{t}_{p}}\quad\quad(3)\]
Çünkü, bu türlerin \({{t}_{p}}\) kadar önceki bir çağda doğanlarının yalnızca küçük bir oranı, \((f=\exp \left( -{{\lambda }_{0}}{{t}_{p}} \right)\), bugüne kadar hayatta kalabilmiştir. Bugün hayatta olan türler için nesil tükenme oranı \({{\lambda}_{0}}\) olduğundan, bu türlerin zamana bağlı olarak, gelecekte \({{t}_{f}}\) kadar zaman sonra nesli tükenenlerinin sayısının zamana bağlı fonksiyonu şu şekildedir:
\[N\left( {{t}_{f}} \right)\text{d}{{t}_{f}}={{N}_{toplam}}{{\lambda }_{0}}\exp \left( -\lambda {{t}_{f}} \right)\text{d}{{t}_{f}}\quad\quad(4)\]
\({{r}_{1}}\) ve \({{r}_{2}}\), [0,1] aralığında düzenli olarak dağılan iki rastgele sayı olsun. Bugün hayatta olan bir tür için aşağıdakiler elde edilir:
\[\begin{align}
& {{t}_{p}}=-{{\left( {{\lambda }_{0}} \right)}^{-1}}\ln {{r}_{1}} \\
& {{t}_{f}}=-{{\left( {{\lambda }_{0}} \right)}^{-1}}\ln {{r}_{2}} \\
& {{r}_{1}}^{({{t}_{f}}/{{t}_{p}})}={{r}_{2}} \\
\end{align}\quad\quad(5)\]
\(Y>0\), bir sabit olmak üzere, aşağıdaki elde edilir:
\[P\left( \left[ {{t}_{f}}/{{t}_{p}} \right]>Y \right)=\int\limits_{0}^{1}{{{r}_{1}}^{Y}d{{r}_{1}}=1/\left( Y+1 \right)}\quad\quad(6)\]
Yukarıdaki olasılık dağılımı, daha önce delta t argümanı olarak adlandırdığımla tam olarak aynıdır. %50 olasılıkla \({{t}_{f}}>{{t}_{p}}\) elde edilir (\(Y=1\) için \(P=0.5\)), %50 olasılıkla \(\frac{1}{3}{{t}_{p}}<{{t}_{f}}<3{{t}_{p}}\) elde edilir (\(Y=3\) için \(P=0.25\) ve \(Y=1/3\) için \(P=0.75\)), ve %95 olasılıkla \(\frac{1}{39}{{t}_{p}}<{{t}_{f}}<39{{t}_{p}}\) elde edilir (\(Y=39\) için \(P=0.025\) ve \(Y=1/39\) için \(P=0.975\)); Fig. 1.’e bakınız.
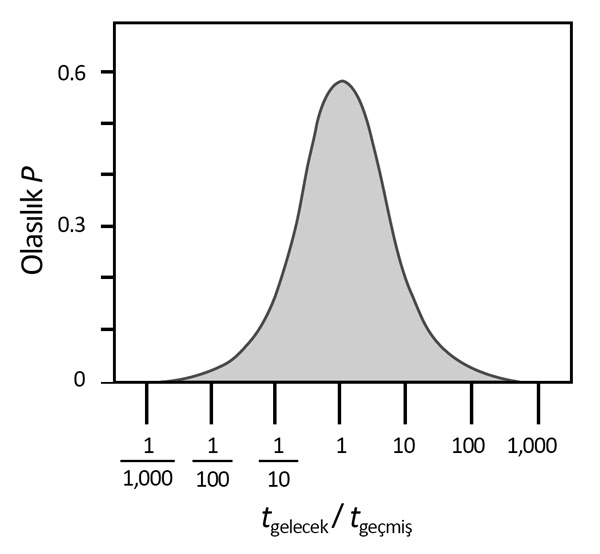
Türümüz, homo saphiens, yaklaşık \({{t}_{p}}\approx 200,000\) yaşındadır. (Bu geleneksel sayıdır, yakın zamandaki bazı tahminler arasında, >100,000 yıl7, >150,000 yıl8, 200,000 yıl9 ve 250,000 yıl6 bulunmaktadır; eğer daha iyi tahminler ortaya çıkarsa, aşikar bir şekilde burada yerine konabilir). Açıktır ki, \({{t}_{p}}\), evrenin yaşı olan \({{t}_{0}}\approx 13\times {{10}^{9}}\) yıldan çok düşüktür. Türümüzün gelecekteki ömrüne ait tahminler için denklem (1)’den denklem (6)’ya kadarki denklemler kullanılırsa, aşağıdaki elde edilir:
\[\begin{gather}
& 5.100\text{yıl}<{{t}_{f}}<7.8\times {{10}^{6}}\text{yıl} \\
& \text{(%95 Güven sınırı)} \\
\end{gather}\quad\quad(7)\]
Bu, türümüz için 0.205 milyon ila 8 milyon yıl arasında bir toplam yaşam süresi verir.
Türlerin çoğu için ortalama yaşam süresi 1 ila 11 milyon yıl10-12 arasında, ve memeliler için 2 milyon yıldır13. Doğrudan atamız olan homo erectus yalnızca 1.4 milyon yıl var olmuş ve yakın akrabalarımız, Neanderthal’lar, yaklaşık 200,000 yıl yaşayabilmişlerdir. Türümüzün, delta t argümanı ile tahmin edilen toplam yaşam süresi ile diğer türlerin, özellikle de bizimkine benzer türlerin, gözlemlenen yaşam süreleri arasında bu şekilde bir büyüklük-mertebesi uyumu vardır. Bu nedenle, zekâmızın, yaşam süremizi diğer türlerinkine göre büyük miktarda artıracağını varsaymamamız gerekir.
Eğer, \({{\lambda }_{0}}\ll {{(200,000\text{yıl})}^{-1}}\) ise, şu anda hayatta olan tüm zeki gözlemcilerin yalnızca küçük bir kısmı, \(f<200,000\text{yıl}\times {{\lambda }_{0}}\ll 1\), \({{t}_{p}}\ll 200,000\)yılını görebilecekti, ve siz, muhtemelen aralarında olmayacaktınız. Türümüzün sonsuza kadar yaşamasını beklediğimiz limitte, \({{\lambda }_{0}}\), 0’a gider ve \(P\left( {{t}_{p}}\ll 200,000\text{yıl} \right)\), 0’a gider. \({{\lambda }_{0}}\)’ın 0’a gittiği limit durumunda gözlemlemeyi bekleyeceğimiz şey, gözlemlediğimiz \({{t}_{0}}\) değerinin sonsuza gitmesidir, \({{t}_{p}}\approx {{t}_{0}}\) ve \(\left( {{t}_{0}}-{{t}_{p}} \right)\ll {{t}_{0}}\). Bunlar, gelecekte belirsiz süre hayatta kalacağımızı belli eden değerler olacaktır. Ancak aslına bakılırsa, tam tersini görüyoruz: \({{t}_{p}}\ll {{t}_{0}}\) ve \(\left( {{t}_{0}}-{{t}_{p}} \right)\approx {{t}_{0}}\). Bunlar yalnızca kısa bir gelecek \({{t}_{f}}\approx {{t}_{p}}\left( \times {{39}^{\pm 1}} \right)\) değerine ulaşacak kadar hayatta kalacağımızı belli eden işaretlerdir.
‘Zeki tür’ kelimelerini, zeki cins, zeki familya, zeki takım veya zeki sınıf ile değiştirebiliriz; argüman yine de olduğu gibi kalır. Böylece, burada türettiğim \({{t}_{f}}\) tahminleri yalnızca bizim için değil, bizim soyumuzdan gelen tüm (delta t argümanına benzer bir argümanla çok sayıda olmaları muhtemel olmayan) zeki türler için (zeki makina türleri de dahil) geçerli olacaktır.
Gould6, \({{t}_{p}}\ll {{t}_{0}}\)’ı, “jeolojideki en korkunç gerçek” olarak isimlendirmiştir, çünkü “eğer insanlık serpilmekte olan bir ağacın küçük bir dalı olarak daha dün ortaya çıktıysa, bu durumda yaşam gerçek anlamıyla bizim için veya bizim yüzümüzden var olmayabilir. Biz, belki de yalnızca, sonradan akla gelen bir fikir, bir tür kozmik kaza veya evrimin yılbaşı ağacındaki tek bir anlamsız süsüz.” Bunu ben de korkutucu buluyorum, ancak başka bir nedenle: Eğer \({{t}_{p}}\ll {{t}_{0}}\) ise, o zaman delta t argümanı, \({{t}_{f}}\approx {{t}_{p}}\left( \times {{39}^{\pm 1}} \right)\) olduğunu ve bu nedenle de \({{t}_{f}}\ll {{t}_{0}}\) olduğunu, yani astronomik zaman ölçeklerinde, biz ve bizim nesillerimiz olan zeki türlerin büyük ihtimalle çok uzun süre var olmayacağına işaret sürer.
Nüfus etkileri. Evren’e ait gözlemleri değerlendirirken, zeki bir gözlemci olmanız gerçeğiyle bağlantılı seçim etkilerini de hesaba katmanız gerekir. Örneğin, zeki gözlemcilerin ortaya çıktığı yerler ve zamanlar, fizik kanunları ile sınırlandırılmış olabilir14. Bu, Carter15 tarafından formüle edilmiş zayıf antropik ilkedir ve aslen yalnızca bir öz-tutarlılık argümanıdır. Argüman, kozmolojide16, 17 dikkate çarpan bir başarı elde ederek, bize Dirac büyük-sayılar çakışmasını14 {İng. coincidence} sağlamıştır. Carter5, Güneş Sisteminin doğuşundan itibaren ölçülen, Yeryüzünde zeki yaşamın ortaya çıkması için gereken zaman, \({{t}_{1}}=4.5\times {{10}^{9}}\text{yıl}\) ile Güneşin gelecekteki ana-bölüm {İng. main-sequence} yaşam süresi \({{t}_{gab}}\approx 6\times {{10}^{9}}\text{yıl}\) arasında dikkat çekici bir mertebe-büyüklüğü çakışması bulunduğunu işaret etmiştir. Carter bu gerçeği, ustalıklı bir argüman ile birlikte kullanarak, zeki yaşamın ortaya çıkması için 1’inci mertebe olasılıksız bir olayın gerektiği sonucuna ulaşmıştır. Buna katılıyorum; dahası, eğer zeki yaşam aslen bir yıldızın ana-bölüm yaşam süresi içerisinde rastgele bir noktada oluştuysa, bu çakışma tam olarak delta t argümanından beklenebilecek bir şeydir. İlginç bir şekilde, Carter’ın argümanı, üstü kapalı bir şekilde burada formüle edilerek ileri sürülen fikre dayanmaktadır: Yani Kopernik İlkesine göre, tüm zeki gözlemciler arasında (henüz doğmamış olanlar da dahil olmak üzere) sizin özel bir yeriniz olmamalı.
Bunu ‘Kopernik antropik ilkesi’ olarak isimlendirelim: şöyle ki, Evrendeki doğum yerinizin uzay ve zamanki konumu, yalnızca zeki bir gözlemci olduğunuz gerçeğinin neden olduğu ölçüde ayrıcalıklıdır (veya özeldir); zeki gözlemciler arasındaki konumunuz ise özel değil, rastgele seçilmiştir. Zeki bir gözlemci olduğunuzu bildiğiniz için, kendinizin, içerisindekilerden herhangi biri olmuş olabileceğiniz tüm zeki gözlemciler (geçmiş, şimdi ve gelecek) kümesi içerisinden seçildiğinizi göz önünde bulundurmanız gerekir.
Bu nedenle insanlara ait kronolojik listede rastgele konumlandığınızı varsayın. \({{N}_{geçmiş}}\) türe dahil belli bir zeki gözlemci doğmadan önceki zeki bireylerin sayısı, \({{N}_{gelecek}}\) daha sonra doğan zeki bireylerin sayısı olmak üzere, eğer türe ait zeki bireylerin toplam sayısı pozitif bir tamsayı \({{N}_{top}}={{N}_{geçmiş}}+1+{{N}_{gelecek}}\) ise, bu durumda, \({{N}_{geçmiş}}\)’in, \({{r}_{1}}\), 0 ve 1 arasında düzenli olarak dağılmış rastgele bir sayı olmak üzere, \({{r}_{1}}\) \({{N}_{top}}\)’a ait tamsayı kısmını oluşturuyor olmasını bekleriz. Böylece, aşağıdaki elde edilir:
\[\begin{gather}
& \left( 1/39 \right){{N}_{geçmiş}}-1<{{N}_{gelecek}}<39\left( {{N}_{geçmiş}}+1 \right) \\
& \text{(%95 Güven seviyesi)} \\
\end{gather}\quad\quad(8)\]
Ve eğer \({{N}_{past}}\gg 1\) ise, aşağıdaki elde edilir:
\[\begin{gather}
& \left( 1/39 \right){{N}_{geçmiş}}\lesssim {{N}_{gelecek}}\lesssim 39{{N}_{geçmiş}} \\
& \text{(%95 Güven seviyesi)} \\
\end{gather}\quad\quad(9)\]
Şimdiye kadar doğmuş olan insanların sayısı 70 milyar mertebesindedir (referans 8-20). Denklem (9)’dan hareket ederek, henüz doğmamış insanların sayısı aşağıdaki şekilde elde edilir:
\[\begin{gather}
& 1.8\text{milyar}<{{N}_{gelecek}}<2.7\text{trilyon} \\
& \text{(%95 Güven seviyesi)} \\
\end{gather}\quad\quad(10)\]
Aşağıdaki örnek modeli ele alalım. Doğum oranı \(b\)’nin sabit bir sayı olduğunu ve ölüm oranının da, \(t_{maks}\) anından önceki zamanlar için \(d_1 < b\) şeklinde sabit bir değeri olduğunu, \(t_{maks}\) anından sonraki zamanlar için de \(d_2 > b\) şeklinde sabit bir değeri olduğunu düşünelim. Böylece nüfus \(p\left( t \right)\), \({{t}_{maks}}\) anından önce \(\text{artış}=b-{{d}_{1}}={{t}_{1}}^{-1}\) oranına ve \({{t}_{maks}}\) anından sonra ise \(\text{düşüş}={{d}_{2}}-b={{t}_{2}}^{-1}\) oranına sahip olacaktır. Böylece, insanların zamana bağlı doğum fonksiyonu aşağıdaki şekilde yazılabilir:
\[\begin{align*}
{{N}_{B}}\left( t \right)dt&=bp\left( t \right) \\
&=b{{N}_{maks}}\exp \left( \left[ t-{{t}_{maks}} \right]/{{t}_{1}} \right)dt \\
&t>{{t}_{maks}}\text{ için} \\
& \\
{{N}_{B}}\left( t \right)dt&=bp\left( t \right) \\
&=b{{N}_{maks}}\exp \left( \left[ {{t}_{maks}}-t \right]/{{t}_{2}} \right)dt \\
&t>{{t}_{maks}}\text{ için} \\
\end{align*}\quad\quad(11)\]
\({{t}_{1}}\)ve \({{t}_{2}}\)’nin değerlerinden bağımsız olarak, gözlemcilerin %50’si, nüfus \(p\left( t \right)\)’nin maksimum değeri olan \({{N}_{maks}}\)’ın 2 katsayı aralığı içerisinde doğmuştur (ve gözlemcilerin %95’i de, nüfus \({{N}_{maks}}\)’ın 20 katsayı aralığı içerisinde doğmuştur). Bu durum, Yeryüzünün şu anki nüfusu 5 milyarın üzerinde olduğunu ve gelecekteki büyümesi hakkındaki birçok izdüşümün nüfusun ~8 ila 12 milyar aralığında21-23 zirve yapıyor olduğunu öngörmesi açısından ilginçtir. Yeryüzü nüfusunun teorik maksimum tahminleri arasında 20 milyar21 ve 40 milyar24 bulunmaktadır. Biyolojik sistemlerde üstel artış ve azalma durumları yaygındır, bu nedenle aşırı nüfus sorunlarının bulunduğu bir çağda doğmuş olmak sizi şaşırtmamalı. \({{t}_{maks}}\)’tan önce doğan insanların toplam sayısı \({{N}_{1}}=b{{N}_{maks}}{{t}_{1}}\) şeklinde ve \({{t}_{maks}}\)’tan sonra doğan kişilerin sayısı da \({{N}_{2}}=b{{N}_{maks }}{{t}_{2}}\) şeklindedir, dolayısıyla \({{N}_{1}}/{{N}_{2}}={{t}_{1}}/{{t}_{2}}\)’dir. \({{t}_{2}}\)’nin sonsuza gittiği limit durumunda, bu model kabaca bir lojistik eğriyi takip eder, bir üstel artış döneminden sonra gelen, doğum ve ölüm oranlarının eşit olduğu uzun bir denge dönemi. Fakat buna izin yoktur, çünkü kendinizi üstel olarak artan kısımda bulursanız \({{N}_{1}}\) kümesinin bir elemanısınızdır, ancak bize gereken, size %2.5’ten daha fazla bir şanslılık atfetmemek için \({{N}_{2}}<39{{N}_{1}}\) olmasıdır; yani, \({{t}_{2}}<39{{t}_{1}}\) şeklindedir, ve siz muhtemelen \({{t}_{f}}\lesssim 39{{t}_{p}}\)’nin geçerli olduğu, \({{t}_{maks}}\)’a daha yakın bir zamanda doğmuşsunuzdur (tıpkı delta t argümanında olduğu gibi). Ancak sizin dahil olmadığınız \({{N}_{2}}\) kümesi, 0 kadar dahi küçük olabilir ve bu da \({{t}_{2}}\)’ye ait tek alt limitin 0 olduğu anlamına gelir. \({{t}_{2}}=0\) limit değerinde (ani nesil tükenmesi), sizin muhtemel (\(P=0.95\)) doğum anınız, sona ait 3.7 ila 0.025 arasındaki ekponansiyel-katlanma {İng. e-folding} anları (\({{t}_{1}}\)) olacaktır ve buradan alt limit \({{t}_{f}}>0.025{{t}_{1}}\approx {{t}_{p}}/40\ln \left( {{N}_{maks}} \right)\) şeklinde ortaya çıkar.
Bir ilk tahmin olarak, makul bir şekilde nüfus çakılmasının, kabaca nüfusun artışını yansıtacağını, belki zamansal bir katsayı ile çarpılmış halde olacağını bekleyebiliriz. Bu durumda üst limit \({{t}_{1}}\) ile ilgili %95 güven seviyesinin, tam olarak delta t argümanında olduğu gibi \(\sim 39{{t}_{p}}\) olmasını bekleriz (çünkü eğer, düşüş, artışı yansıtmış fakat 39 katsayısı ile yayılmış olsaydı, doğan kişilerin 39/40’ının, eğrinin azalan kısmında doğmuş olmaları gerekirdi). üzerindeki %95-güven-seviyesine ait alt limit, doğrudan, gelecek insan doğumlarına ait %95-güven-seviyesi alt limiti olan 1.8 milyardan hesaplanabilir (denklem (10)). Şu anki hızla25 1.8 milyar insanın daha doğması için gereken süre yalnızca 12 yıl kadardır (doğumların ani bir nesil tükenmesinden önce azalmadan devam ettiği varsayılırsa). Bu aşırı derecede kötümser olan alt limit için iki parça kötü şansın aynı anda gerçekleşmesi gerekir, %2.5 diliminde bulunma talihsizliği ile birlikte neslin aniden tükenmesi. Yılların sayısı bu denli azdır çünkü şimdiye kadar yaşamış insanların hatırı sayılır bir oranı, %7.7’si, halihazırda hayattadır18-20, 25. Bu tehlikeli bir durumdur. Böylece nüfus etkilerini de göz önünde bulundurarak aşağıdaki değer elde edilir:
\[\begin{gather}
& 12\text{milyon yıl}<{{t}_{f}}<7.8\text{milyon yıl} \\
& \text{(%95 Güven seviyesi)} \\
\end{gather}\quad\quad(12)\]
Üzücü bir şekilde, \({{t}_{1}}\)’e ait aşırı derece düşük değerler dahi güvenilir bir şekilde göz ardı edilemez (\(P=0.95\)), ancak \({{t}_{f}}\)’ye ait yüksek değerler, örneğin ulaşmayı umduğumuz milyar yıllar, edilebilir.
Ehrlich ve Ehrlich24, insan ırkı için olası üç gelecek senaryosu ileri sürmektedir:
(1) bir sonraki yüzyılda 10 milyarı geçtikten sonra azalarak yok olmak;
(2) bir sonraki yüzyılda 10 milyarı geçip, ardından birkaç yüz bin kişiye düşerek 4 milyon yıl boyunca kaynakları bakımından fakirleşmiş bir gezegende idareli bir şekilde yaşamak; ve
(3) önümüzdeki 4 milyon yıl boyunca sürdürülebilecek 1 milyarlık bir nüfus ile yaşamak.
Bu senaryoların ima ettiği gelecek doğum oranları, yaklaşık olarak, (1) için 10 milyar, (2) için 30 milyar ve (3) için \(40\times {{10}^{12}}\)’dir. Ne yazık ki, yalnızca (1) ve (2)’deki kötümser senaryolar denklem (10) ile belirtilen limitler içerisinde kalmaktadır (Fig. 2’ye bakınız). \({{N}_{gelecek}}<2.7\times {{10}^{12}}\) (denklem (10)) ile yılda 145 milyon doğum25 birleştirildiğinde, doğum oranları düşmediği takdirde \({{t}_{f}}<19,000\text{yıl}\)olduğunu buluruz. Eğer hayatta kalma süremizi 7.8 milyon yıldan (denklem (12)’den) öteye taşımak istiyorsak, doğum oranlarını 400 kattan fazla azaltmamız gerekiyor. İyimser biri, bunun genetik mühendislik sayesinde büyük ölçüde uzatılacak yaşam süresi gibi sıra dışı yöntemlerle elde edilebileceğini umut ediyor olabilecek olmasına rağmen, kötümser biri, kendi beklenen yaşam süresinde yüksek bir doğrusal artış elde edebilme gücüne sahip bir uygarlığın, kendi nüfus miktarında üstel artış elde etme gücüne de sahip olacağını fark edecek ve bu tür bir düşüşün bir nüfus çakılması ile çok daha kolay bir şekilde ortaya çıkacağını iddia edecektir.
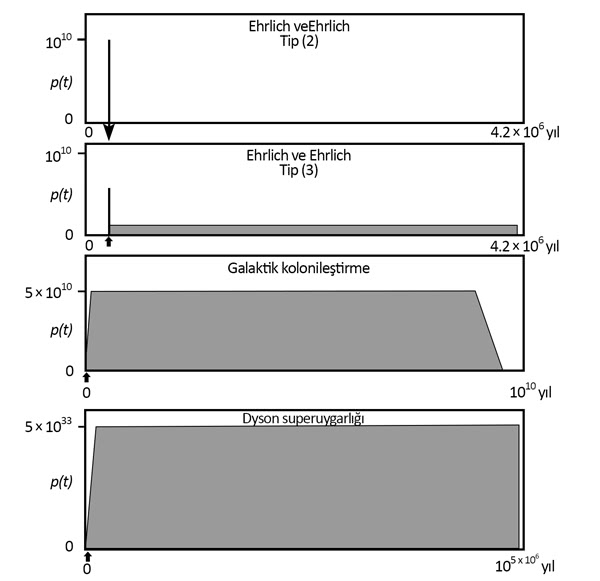
Denklem (9), sizin muhtemelen insanlığa ait kronolojik listede ilk %2.5’lik kısımda veya son %2.5’lik kısımda olmadığınıza işaret eder. Bu sonuçtan, ilerleme seviyesi denklem (9)’un bilinebileceği kadar yüksek olan bir çağda doğduğunuz için listede özel bir yeriniz bulunduğunu iddia ederek kaçınabilir misiniz? Şimdi, eğer şu an 12 yaşından büyükseniz, daha şimdiden 1.8 milyar kişiden fazlası sizden sonra doğmuş demektir, böylece kronolojik listenin son %2.5’inde olmadığınızı halihazırda biliyorsunuz. Şu anki doğum oranlarıyla bir 12 yıl daha sonra, şu an hayatta olan herkes kronolojik listenin son %2.5’luk kısmından çıkmış olacak. Dolayısıyla, listenin son %2.5’lik kısmında olmanız için bir kötü şans etmeni gerekli. Eğer iyimser biriyseniz ve uygarlığın devam edeceğini ve artarak ilerleyeceğini düşünüyorsanız, bu durumda gelecekteki tüm insanların denklem (9)’u bilebileceği veya türetebileceği kadar ilerlemiş uygarlıklar içerisinde yaşayacak olmaları gerekir; bu yüzden denklem (9)’u uygulayabilecek kadar ilerlemiş çağlarda yaşayan tüm gözlemcilerin %2.5’inden daha azı kronolojik listenin ilk %2.5’lik kısmında bulunabilir (çünkü listenin başındaki bir parça hariç tüm listeyi kaplarlar).
Böyle iyimser bir senaryoda, eğer \({{N}_{gelecek}}>2.7\times {{10}^{12}}\) ise, kendinize neden denklem (9) ve çeşitlemelerinin biliniyor olacağı çağlar içerisinde yaşayacak \(2.7\times {{10}^{12}}\) insan arasında, keşfedildiği sırada hayatta olan 5.4 milyar kişi arasında olacak kadar şanslı (\(P=0.002\)) olduğunuzu sormanız gerekecekti. Örneğin, Kopernik’e ait teorinin bilindiği bir çağda yaşıyorsunuz, fakat keşfedildiği sırada hayatta olacak kadar şanslı da değilsiniz, ve bu denli iyimser bir senaryoda denklem (9)’a göre aynı konumda olmanız muhtemel olacaktı. Sizi kronolojik listenin ilk %2.5’lik kısmı içerisinde kalmaya zorlamak için tek durum, uygarlığın yakın gelecekte çöktüğü ve tıpkı daha önceki gibi, uzun süre devam etmesi umulacak, (denklem (9)’u unutan ve tekrar türetecek kadar ileri olmayan) bir avcı-toplayıcı evresine döndüğümüz türde bir tip (2) senaryosunda yaşıyor olmanızdır. Fakat bu da işe yaramaz, çünkü uygarlık olmadan neslimizin tükenmesine karşı özellikle korunuyor olma olasılığını yitiririz ve bu noktada, diğer insansı türler gibi, gelecekteki yaşam süremiz olarak 2 milyon yıl veya daha azını beklememiz gerekir. Bu nihai acı-toplayıcı evresindeki nüfusun gelecekteki doğumlarının (denklem (9) ile tutarlı bir şekilde) 30 milyar mertebesinde olacak kadar düşük olması gerekir. (Böyle bir durumda, Carter’ın5 argümanına göre, uygarlık, türün yaşam süresi içerisinde rastgele bir noktada oluşmalı ve delta t argümanı geçerli olmalıdır.) Tüm bu durumlarda, kronolojik listenin ilk %2.5’lik kısmında olmak en az %2.5’lik bir iyi şans gerektirir.
Teknolojik bir uygarlıkta yaşıyor olduğumuz gerçeği üzerine kurulu tüm yargıların her durumda düşük olmasını bekleriz, çünkü teknolojik uygarlıklar sırasında nüfus o kadar yüksektir ki, zeki gözlemcilerin önemli bir bölümünün bu sırada doğmuş olmaları beklenir.
Uzak gelecekle ile ilgili beklentiler
(Nüfusumuzu en az en az \({{10}^{9}}\) kat artırarak) Galaksiyi kolonileştirmemiz olasılığı \(P\lesssim {{10}^{-9}}\) mertebesindedir, çünkü böyle bir durumda \({{N}_{gelecek}}>{{10}^{9}}{{N}_{geçmiş}}\) ve \(P\left( {{N}_{gelecek}}>{{10}^{9}}{{N}_{geçmiş}} \right)\lesssim {{10}^{-9}}\) olmasını bekleriz. (Başka dünyalara mikroorganizma26 tohumları yerleştirebiliriz, ancak Carter’ın5 argümanına göre bunların yalnızca küçük bir kısmında zeki yaşam ortaya çıkacaktır. Yeryüzündeki yaşama ait tohumların bu şekilde atılmış olmasının düşünüldüğü durumda bile26-28, birkaç milyar yıllık karakteristik gecikme, bu gerçekleştiği sırada soyumuzda doğrudan ‘atamız’ olan uygarlıklardan en fazla birkaç tane olmasını garantiler, ve, delta t argümanına benzer bir argüman kullanılırsa, bizim ‘torunlarımız’ olan zeki türlerin sayısının da yüksek olması olası değildir). Güneş’in etrafını çeviren O’Neill30 güneş enerjili uzay kolonilerinden oluşan bir Dyson29 küresi inşa etme (Güneş’in tüm ışıma enerjisini kullanma ve nüfusumuzu en az \({{10}^{8}}\) katsayısı ile artırma) olasılığımız \(P\lesssim {{10}^{-8}}\) mertebesindedir. Tüm galaksisindeki enerji çıktısını her yıldızın etrafına birer Dyson küresi yerleştirerek kullanması şeklinde tanımlanan Kardashev tip III{*} uygarlığı kurma (ve nüfusumuzu en az \({{10}^{17}}\) katsayısı ile artırma) olasılığımız \(P\lesssim {{10}^{-17}}\) mertebesindedir.
Dyson31, zeki yaşamın prensipte, Evren genişledikçe giderek daha düşük ve daha düşük sıcaklıklarda (giderek daha yavaş düşünerek, ve kış uykusu dönemleri arasına serpiştirilmiş şekilde) işleyerek sonsuza kadar devam edebileceğini, sınırlı miktardaki enerji ile sınırsız sayıda düşünceye sahip olabileceğini gösterdi. Bir örnek olarak, Evrenimizin normal genişlemesine \(\sim {{10}^{5\times {{10}^{6}}}}\) yıl devam edebileceği Linde’nin32 kaotik enflasyon33 kozmolojisini düşünün. Geçen etkin bilinçli süre miktarı, yavaş düşünme ve kış uykusu nedeniyle \({{10}^{1.25\times {{10}^{6}}}}\) yıl olurdu. Linde modelinde, {kozmik} ufuk içerisindeki kütle miktarı \({{10}^{5\times {{10}^{6}}}}\) yıla kadar doğrusal bir şekilde artabileceği için, yaşanabilir bir gezegendeki zeki yaşam oluşumu için aşırı derecede kötümser bir olasılık için bile (diyelim ki \({{10}^{-4,000}}\)) yine de enflasyon bölgemizin tamamını ele alırsak, eninde sonunda görünür hale gelecek \({{10}^{5\times {{10}^{6}}}}\) mertebesindeki sayılarda zeki uygarlıklar olacaktır. Beklenen yaşam süresi \({{10}^{2}}\) kesintisiz yıldan daha uzun olan zeki gözlemcilerin bütüne egemen olmalarının fazla bir sıklıkla yaşamıyor olması gerekir, aksi takdirde, siz de muhtemelen bunlardan biri olurdunuz. Cinayet ve intihar dışındaki tüm ölüm nedenlerini ortadan kaldırmak, beklenen yaşam sürelerini ancak \({{10}^{4}}\) yıla kadar artırırdı, hatta yaşam sürelerindeki sıra dışı artışlar (diyelim ki \({{10}^{100}}\) bilinçli yıla kadar), yine de Dyson süperuygarlığının zaman içerisinde \({{10}^{1.25\times {{10}^{6}}}}\)mertebesinde birey sayısına sahip olmasını gerektirecekti ve bizim bir Dyson süperuygarlığına dönüşme olasılığımız da \({{10}^{-1.25\times {{10}^{6}}}}\) mertebesinden daha düşük olacaktı; yine de Evrende \(\sim {{10}^{3.75\times {{10}^{6}}}}\) kadar Dyson süperuygarlığı bulunuyor olabilir. Yani, bazı zeki yaşamlar uzak gelecekte hayatta kalıyor olabilir; yalnızca bizim veya torunlarımızın onlardan biri olma olasılığı düşüktür. (Kozmoloji izin verdiği takdirde) bir süperuygarlığın sonsuz bilinçli zaman geçirmiş olması ve sonsuz zeki gözlemciye (\({{N}_{top}}\)) sahip olmuş olmasına ait limitte, bizimki gibi sıradan uygarlıkların süperuygarlıklara dönüşme oranının sıfıra gitmesi gerekir bu nedenle de kendi orijinal gezegenlerinde doğmuş gözlemciler, tüm zeki gözlemciler kümesi içerisinde sonsuz küçük bir azınlık değildir.
SETI ile ilgili çıkarımlar
Kolonileştirme, galaktik kolonistlerin ve onların torunlarının Evrendeki zeki gözlemcilerin sayılarına egemen olma konusunda önemli değildir (aksi takdirde onlardan biri olmanız muhtemel olurdu). Bu bizim dünya-dışı varlıklar tarafından kolonileştirilmemiş olmamız konusunda neden şaşırmamamız gerektiğini açık bir şekilde34 gösteriyor. Galakside \({{10}^{9}}\) yaşanabilir gezegen olduğunu varsayın (iyimser olduğu açık). Carter’ın5 argümanı, bunlardan zeki yaşamın ortaya çıkacakların oranının büyüklük mertebesinin en az 1 ve hatta belki de 1’den kat kat az olduğunu göstermiştir. Yıldızlarının ana-bölüm yaşam süresi \({{t}_{ab}}\), \({{10}^{10}}\) mertebesinde olduğu için , zeki uygarlıkların Galakside oluşma oranı \(\eta <0.01{{yıl}^{-1}}\) şeklindedir. Eğer bu uygarlıkların radyo yayınlarının yaşam süresi \(\left\langle L \right\rangle \) ise, bu durumda (kolonileştirme önemli olmadığı için) Drake denkleminden35, 36, Galaksimiz içerisinde şu an \({{N}_{0}}=\eta \left\langle L \right\rangle <0.01{{yıl}^{-1}}\left\langle L \right\rangle \) sayıda uygarlığın radyo yayını yaptığını gözlemleyebiliyor olmayı bekleriz. Radyo yayını yapan bir uygarlıkta doğmuş olduğunuz için, radyo yayını yapan uygarlıklardaki gözlemciler kümesinden rastgele seçilmeniz gerekir. Bizim radyo yayınımıza ait yaşam süresinin \({{L}_{1}}\) olduğunu varsayın (radyo yayını, neslimiz tükendiği için, teknolojik uygarlık sona erdiği için veya yalnızca daha başka bir iletişim yöntemine geçtiğimiz için sona erebilir). Bu durumda delta t argümanından, Yeryüzünde geçmişteki radyo yayınına ait yaşam süresi \({{L}_{p}}=105\text{yıl}\) ve \({{r}_{1}}\), 0 ile 1 arasında düzenli bir şekilde dağılımı olan rastgele bir sayı olmak üzere, \({{L}_{p}}={{r}_{1}}{{L}_{j}}\) olduğunu biliyoruz. \(N\) sayıdaki radyo yayını yapan uygarlıkları öyle sıralayalım ki tüm \(i\)’ler için, \({{L}_{i}}\le {{L}_{i+1}}\) olsun. Radyo yayını yapan bir uygarlıktaki zeki gözlemcilerin sayısının \(L\) ile orantılı olduğunu varsayalım (bu bir uygarlığa ait doğum oranları ile \(L\) arasında bir korelasyon olmadığını varsaymaya eşdeğerdir; eğer aralarında, pozitif korelasyon olsaydı, ki bu doğal görünebilir, o zaman limitler daha da güçlü olacaktı). Gözlemciler listesinde rastgele konumlandığınız için, aşağıdaki elde edilir:
\[\begin{align}
\sum\limits_{i=1}^{I}{{{L}_{i}}}&={{r}_{2}}\sum\limits_{i=1}^{N}{{{L}_{i}}}={{r}_{2}}\left\langle L \right\rangle N \\
& \le j{{L}_{j}}\le N{{L}_{j}}=N{{L}_{p}}/{{r}_{1}} \\
\end{align}\quad\quad(13)\]
Burada, \({{r}_{2}}\), 0 ile 1 arasında düzenli dağılımı olan rastgele bir sayıdır. Böylece, aşağıdaki elde edilir:
\[\left\langle L \right\rangle \le {{L}_{p}}/\left( {{r}_{1}}{{r}_{2}} \right)\quad\quad(14)\]
\(\left( {{r}_{1}}{{r}_{2}} \right)>0.0087\) olma olasılığı \(P=0.95\) şeklindedir, böylece, aşağıdaki elde edilir:
\[\begin{gather}
& \left\langle L \right\rangle \le 12,000\text{ yıl, }{{N}_{0}}<121 \\
& (\text{%95 güven seviyesi}) \\
\end{gather}\quad\quad(15)\]
Bu, \(L\)’lerin dağılım şeklinden bağımsız ve Cameron’un37 tahmini olan \(\left\langle L \right\rangle ={{10}^{6}}\)yıl değerinden hatırı sayılır ölçüde düşüktür.
Bu nedenle, radyo araştırmalarının Galaksimizdeki veya diğer galaksilerdeki diğer uygarlıklar konusunda başarılı olma ihtimali vardır, ancak en yakınımızdaki 1,000 yıldız için yapılan radyo araştırmalarının başarılı olması muhtemel değildir. \({{N}_{0}}\) için üst sınır yüksektir çünkü, bizim benimsediğimiz birden yalnızca bir mertebe düşük olan iyimser olasılığa nazaran, Carter’ın5 argümanı, yaşam süresinin ana-bölümü boyunca verili bir yıldız etrafındaki, yaşanabilir bir gezegende zeki türlerin ortaya çıkma olasılığının birden pek çok mertebe düşük olduğunu ima eder.
Bugün hayatta olan bir insan olarak, nüfusunun medyan değer olan 6.3 milyondan25 daha yüksek olan bir ülkede doğmuş olma olasılığınız yüksektir (\(P=0.97\)). Aynı nedenle, etkileşime girmeyen fırsatçı türlerden bekleyebileceğimiz gibi, eğer zeki türlerin nüfuslarında geniş bir yayılım mevcut ise, o zaman sizin, rastgele bir zeki gözlemci olarak, nüfusu medyandan yüksek olan bir zeki tür içerisinde bulunmanız olası olacaktı. (Gözlemlenen çeşitli tür-bolluk eğrilerine en iyi şekilde uyan standart, \(a=0.2\) lognormal dağılımda, bireylerin %98.6’sı, medyan değerin üzerinde nüfusu olan türlere aittir)38-42. Bireylerinin, toplam birey sayısına egemen olmaması için, bizimkinden hatırı sayılır ölçüde büyük olan uygarlıkların oldukça nadir olmaları gerekir. Bu nedenle, Galaksimiz içerisinde bir Dyson küresi, veya gözlemlenebilir ufukta bir Kardashev tip III uygarlığı görmeyi beklemiyoruz.
Uzay Yolculuğu ile ilgili çıkarımlar
Hayatta kalma beklentilerimiz açısından yaşam alanımızı genişletme konusunda çok iyi olacak olmasına rağmen ve uzaya çıkmayı halihazırda biliyor olmamıza rağmen, neden Galaksiyi kolonileştirme olasılığımız bu kadar düşük? Yaklaşık 200,000 yıldır var olmamıza rağmen, uygarlık (şehirler ve yazı ile birlikte) yalnızca 5,000 yıldır var ve teknolojik uygarlık, yalnızca 32 yıldır uzay yolculuğu yapabilecek kadar ilerlemiş durumda. Delta t argümanı, sahip olduğumuz uzay yolculuğuna çıkma kabiliyet ve güdülenmesinin yalnızca bir diğer 32 yıl (\(\times {{39}^{\pm 1}}\)) mertebesinde daha sürme ihtimali olduğunu gösteriyor. Daha en baştan uzay yarışına neden olmuş olan Soğuk Savaş artık bitti. Ay’a olan insan uçuşları yalnızca dört yıl sürdü ve uzaydaki insan aktivitesi Yeryüzünün düşük yörüngelerine çekildi. Delta t argümanı, gerçekleştirilmeye devam ettiği esnada, prensip olarak, koloni kurma (ve bu sayede de daha fazla koloni kurma) kabiliyeti sağlayan uzay yolcuğu için yalnızca kısa süreli bir fırsatımız aralığımız olabileceğini gösterir. Eğer bu fırsat aralığının, kendisinden faydalanamadan geçmesine izin verirsek, eninde sonunda neslimizin tükeneceği Yeryüzünde kalmak zorunda kalacağız. Şimdiye kadar, Yeryüzünün kütleçekim potansiyel kuyusu dışında, tek bir insan dahi doğmadı.
Burada kullandığım yöntemler son derece ölçülüdür; eğer sonuçları dramatikse, bu yalnızca gerçeklerin dramatik olmasından kaynaklanır (\({{t}_{p}}\ll {{t}_{0}}\)). Bu makale yalnızca sizin rastgele bir gözlemci olduğunuz hipotezini işaret eder ve savunur. Bazen geleceğin öngörülemez olduğunu söyleriz. Bu başka bir açıdan, doğduğunuz sırada, oransal olarak insanlara ait kronolojik listenin neresinde bulunmuş olacağınıza dair hiçbir bilginin olmaması olarak da görülebilir. En nihayetinde, insanlara ait kronolojik listenin ilk %2.5’lik kısmında bulunma olasılığınız, yaşadığınız şehrin telefon rehberindeki kişilerin alfabetik sırasında ilk %2.5’te bulunma ihtimalinizden daha olası değildir. Elimizde diğer zeki türlerin yaşam süreleri konusunda gerçek veriler olmadığı için, tartışmaya açık bir şekilde, öne sürebileceğimiz en iyi hipotez budur. Şu anda elimizde bu hipotezi reddetmemize yetecek kadar veri bulunmuyor ve hipotez, bazı gerçekleri açıklayabiliyor: Bir yüksek nüfus döneminde doğmuş olmanız ve Yeryüzünün dünya dışı varlıklar tarafından kolonileştirilmemiş olması. Tüm iyi bilimsel hipotezler gibi, bu hipotez de, derhal yakın bir yıldız etrafındaki bir uygarlığa ait zeki radyo sinyallerinin keşfedilmesi veya ileride \(2.7\times {{10}^{12}}\)’den fazla insanın doğmuş olması ile, yanlışlanabilirdir. Eğer, bizim zeki torunlarımızın 10 milyar yıl var olacağına ve Galaksiyi kolonileştireceğine inanıyorsanız, aynı zamanda, en sonunda, sizin de bizim zeki soyumuza ait üyelerin ilk küçük kesrinde var olmuş olacak kadar şanslı olduğunuza da inanmanız gerekir (Fig. 2’ye bakınız). Eğer kendinizi telefon rehberinin ilk sayfasında bulacak kadar, veya hatta 1 Ocak’ta doğmuş olacak kadar bile şanslı değilseniz, nihai kronolojik listede şansınızın bundan daha bile fazla yaver gitmiş olduğunun ortaya çıkacağını içiniz rahat bir şekilde varsayabilir misiniz? Hemen yarın piyangoyu kazanacağınız veya elinize ulaşan bir mektup zincirine katılım göstererek zengin olacağınız iddialarında olduğu gibi, gelecekte yaşanacak olayların gizlice, en sonunda sizin sıra dışı ölçüde şanslı biri olduğunuzun ortaya çıkacağı şekilde işlediği gibi bir iddia konusunda da şüpheci olmanız gerekir.
Peki ya Yeryüzündeki yaşamın tümünün geleceği ne olacak? Darwin43 şöyle demiştir:
“Ve şu anda hayatta olan türlerin pek azı herhangi bir şekilde soyunu çok uzak geleceğe iletebilecektir . . . . Tüm yaşayan canlı biçimleri Silüriyen çağdan çok önce yaşamışların doğrudan torunları olduğu için, nesiller arasındaki sıradan geçişin bir kez bile olsun kesintiye uğramamış olduğu ve hiçbir tufanın tüm dünyayı harap etmemiş olduğu konusunda emin olabiliriz. Bu nedenle, eşit derecede ölçülemeyecek kadar uzun bir geleceği, belli bir güvenle bekleyebiliriz”
[italikler bana ait]. Bu özünde, delta t argümanının Yeryüzündeki tüm canlılar arasındaki konumumuza uygulanmış halidir. Eğer önümüzdeki birkaç milyon yıl içinde türümüzün nesli tükenirse ve uzayı kolonileştiremezsek ve Yeryüzündeki tüm hayatı yok etmeye muktedir de değilsek, o zaman gerçekten (daha ilginç olmamıza rağmen) diğer türler gibi olabiliriz ve Yeryüzündeki yaşam içerisinde gerçekten rastgele bir konumda bulunuyor olmamız beklenebilir. Yeryüzündeki yaşam 3.6 milyar yıl önce başladı ve onun, denklem (1)’e uygun ve Darwin’in öngördüğü şekilde, Güneş bir kırmızı deve dönüşene kadar bir 6 milyar yıl daha devam etmesini bekleyebiliriz.
Galaksiyi kolonileştirme ve uzak geleceğe kadar hayatta kalabilme konusundaki ihtimallerin düşük olmasının nedeni, bunların doğaları gereği kabiliyetimizin ötesinde olmasından değil, canlıların genellikle maksimum potansiyellerini ortaya koyamamasından kaynaklanmaktadır. Zekâ, maksimum kapasitesinde kullanabilirsek bize, prensipte muazzam bir potansiyel kazandıracak bir kabiliyettir; ancak okyanusta yaşayan ay balığının {Lat. mola mola} yaptığı gibi 30 milyon yumurta bırakabilme kabiliyeti de öyledir44. Arzu ettiğimiz kadar başarılı olabilmek için, çoğu zeki türlerin yapmadığı, gerçekten dikkate değer bir şeyler yapmamız gerektiğini (uzayı kolonileştirmek gibi) aklımızda bulundurmamız gerekiyor.
Bu makaleyi tamamladıktan sonra, gelecekteki insan nüfusu konusunda burada verilenlere benzer fikirlerin, yazılı hale gelmemiş olsa da, Brandon Carter tarafından 1983 yılındaki bir konuşmada tartışıldığını (Leslie45-47 tarafından yapılan değerlendirmeye bakınız), aynı zamanda da bağımsız olarak Nielsen48 tarafından ileri sürüldüğünü öğrendim.
Kaynaklar
1. Gamow, G. Phys. Rev. 74, 505-506 (1948). geri=>
2. Alpher, R. A. & Herman, R. C. Nature 162, 77 4-775 (1948). geri=>
3. Penzias, A. A. & Wilson, R. W. Astrophys. 1 142, 419-421 (1965). geri=>
4. Mather, J. C. et al. Astrophys. J. 354, L37 -L40 (1990). geri=>
5. Carter, B. Phil. Trans. R. Soc. A310, 34 7-363 (1983). geri=>
6. Gould, S. J. Wonderful Life, 44-320 (Norton, New York. 1989). geri=>
7. Caroll, R. Vertebrate Paleontology and Evolution, 475-476 (Freeman. New York. 1988). geri=>
8. Stringer. C. B. Scient Am. 263, 98-104 (1990). geri=>
9. Cann, R. L., Stoneking, M. & Wilson. A. C. Nature 325, 31-36 (1987). geri=>
10. Wilson, E. 0., Biodiversity (ed. Wilson, E. 0.) 8 (National Academy Press. Washington DC. 1988). geri=>
11. Raup, D. M. Biodiversity (ed. Wilson, E. 0.) 54 (National Academy Press, Washington DC, 1988). geri=>
12. Raup, D. M. Science 231, 1528-1533 (1986). geri=>
13. Stanley, S. M. Proc. natn. Acad. Sci. 72, 646-650 (1975). geri=>
14. Dicke, R. H. Nature 192, 440-441 (1961). geri=>
15. Carter, B. Confrontation of Cosmological Theories with Observation (ed. Longair. M. S.) 291-294 (Reidel. Dordrecht, 1974). geri=>
16. Carr, B. J. & Rees, M. J. Nature 278, 605-612 (1979). geri=>
17. Barrow, J.D. & Tipler, F. J. The Anthropic Cosmological Principle, 231-248 (Clarendon. Oxford, 1986). geri=>
18. Desmond, A. Population Studies: Selected Essays and Research (ed. Kammeyer, K. C. W. 436-450) (Rand McNally, Chicago, 1969). geri=>
19. Brraben, J-N. Population 34e Annee. no. 1,13-25 (1979). geri=>
20. Thatcher. A. R. Guiness Book of World Records 1991 (ed. Mcfarlan. D.) 202 (Facts On File, New York. 1990). geri=><
21. McEvedy, C. & Jones. R. Atlas of World Population History, 351 (Penguin, Middlesex. 1978). geri=>
22. Demeny, P. World Population and U.S. Policy (ed. Menken. J.) 65 (Norton, New York, 1986). geri=>
23. United Nations Population Projections: Problems and Solutions, Workshop on Population Projections. Budapest, 1980, 118 (United Nations. New York. 1981). geri=>
24. Ehrlich, P. R. & Ehrlich, A. H. The Population Explosion 16-237 (Simon and Schuster. New York. 1990). geri=>
25. Haub, C .. Kent. M. M. & Yanagishita. M. 1991 World Population Data Sheet (Population Reference Bureau, Washington DC. 1991). geri=>
26. Crick, F. H. C. & Orgel, L. E. Icarus 19, 341 (1973). geri=>
27. Arrhenius. S. Die Umschau 7, 481 (1903). geri=>
28. Gold, T. Air Force and Space Digest, May, 65 (1960). geri=>
29. Dyson, F. J. Science 131, 1667-1668 (1960). geri=>
URL: //bilimvesaire.com/2017/03/bilim/dyson-kureleri-nedir-nasil-aramak-gerekir/
30. O’Neill, G. K. Physics Today 27, 32-40 (Sept. 1974). geri=>
31. Dyson. F. J. Rev. mod. Phys. 51, 447-460 (1979). geri=>
32. Linde. A. D. Inflation and Quantum Cosmology, 139-141 (Academic, Boston, 1990). geri=>
33. Guth, A. H. Phys. Rev. D23, 34 7-356 (1981). geri=>
34. Hart, M. H. & Zuckerman, B. Extraterrestrials- Where Are They? (Pergamon, New York. 1982). geri=>
35. Drake, F. & Sobel, D. Is Anyone Out There? 52-68 (Delacorte, New York. 1992). geri=>
36. Shklovskii, I. S. & Sagan. C. Intelligent Life in the Universe. 409-418 (Dell, New York, 1966). geri=>
37. Cameron, A. G. W. Sky and Telescope 26, 258-261 (1963). geri=>
38. May, R. M. Ecology and Evolution of Communities (eds Cody, M. L. & Diamond, J. M.) 81-120 (Harvard Univ. Press, Cambridge, MA, 1963). geri=>
39. Preston. F. W. Ecology 29, 254-283 (1948). geri=>
40. Preston, F. W. Ecology 43, 185-215 (1962). geri=>
41. Preston. F. W. Ecology 43 410-432 (1962). geri=>
42. Whittaker, R. H. Taxon 21, 213-251 (1972). geri=>
43. Darwin, C. On the Origin of Species, 1859 (reprinted by Harvard Univ. Press. Cambridge, MA, 1964). geri=>
44. McFarland. D. Guinness Book of World Records 1 991, 42 (Facts On File, New York. 1990). geri=>
45. Leslie, J. Bull. Canad. nucl. Society, 10 (3). 10-15 (1989). geri=>
46. Leslie, J. The Philosophical Quarterly, 40, 65-72 (1990). geri=>
47. Leslie, J. Mind 101.403 521-540 (1992). geri=>
48. Nielsen, H. B. Acta phys. Polan. 820, 427-468 (1989). geri=>
-oOo-