Bernhard Riemann tarafından öne sürülen Riemann Hipotezi nihayet kanıtlanıyor olabilir
Bernhard Riemann tarafından yaklaşık 160 yıl önce sürülen Riemann Hipotezi, yeni çalışma ile kanıtlanmaya biraz daha yaklaştı…
Sayılar teorisinin en önemi parçalarından birini, ala sayılar oluşturuyor. Bu sayılar, kendilerinden ve 1’den başka sayılarla ifade edilemezken, geri kalan tüm sayıların yapıtaşlarını veya “atomlarını” oluşturuyor.
Asal sayılar, özellikle internet güvenliğinde, bağlantıların şifrelenmesi gibi önemli konularda büyük rol oynuyor olmalarına rağmen, henüz asal sayıları verecek kesin bir formül veya asal sayıların ne sıklıkla ortaya çıkacaklarını veren kanıtlanmış bir ifade bulunmuyor.
Ancak, asal sayıların ortaya çıkış sıklığı ile ilgili önemli bir hipotez mevcut. Alman matematikçi Bernhard Riemann tarafından 1859 yılında öne sürülen hipoteze göre, Riemann zeta fonksiyonunun, sıfır değerini aldığı noktalar, asal sayıların ortaya çıkış sıklıklarını belirlemek için kullanılabiliyor. Ancak aradan geçen 160 yıla rağmen, bu hipotez henüz kanıtlanabilmiş değil. Clay Mathemetics Institute, milenyum ödülleri kapsamında, çözümü bulana 1.000.000 dolar vadediyor olmasına rağmen…
Aslına bakarsanız, Clay Mathemetics Institute tarafından öne sürülen problem çok basit görünüyor:
Bazı sayılar, daha küçük sayıların çarpımı olarak ifade edilememek gibi bir özelliği var, örneğin, 2, 3, 5, 7 gibi. Bu sayılara asal sayılar deniyor ve saf matematik ve uygulamalarında önemli rol oynuyorlar. Asal sayıların, tüm sayılar içerisindeki dağılımları, normal bir düzene göre değil. Ancak, Alman matematikçi G. F. B. Riemann’ın (1826-1866) çalışmalarına göre, asal sayıların ortaya çıkış sıklığı, Riemann Zeta Fonksiyonu adı verilen bir fonksiyonun davranışıyla yakından ilgili,
ζ(s) = 1 + 1/2s + 1/3s + 1/4s + …
Riemann hipotezi ile iddia edilene göre,
ζ(s) = 0
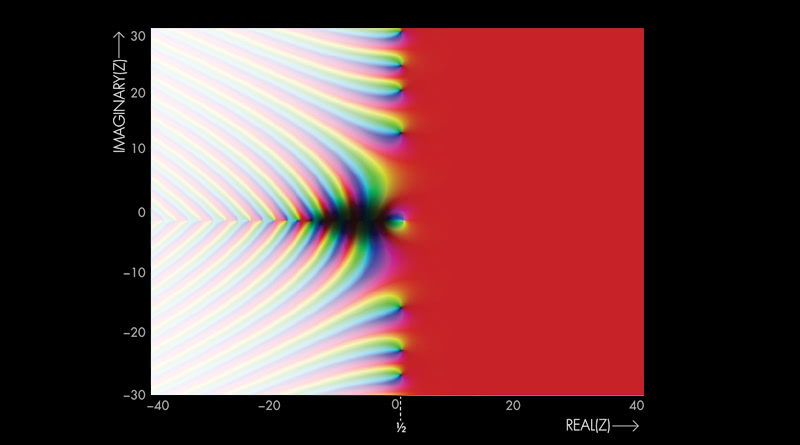
ifadesine ait, aşikâr olmayan tüm çözümler, dikey bir doğru üzerinde yer almaktadır.
Bu iddia, ilk 10,000,000,000,000 çözüm için kontrol edilmiş durumdadır. Bunun tüm aşikâr olmayan çözümler için doğru olduğuna dair bir kanıt, asal sayıların dağılımı hakkındaki gizeme ışık tutacaktır.
Burada bahsi geçen Riemann zeta fonksiyonu şu şekilde tanımlanıyor:
$$\zeta \left( s \right) = \sum\limits_{n = 1}^\infty {{1 \over {{n^s}}}} $$
Peki “aşikâr çözüm” ve “aşikâr olmayan çözüm” nedir? Riemann zeta fonksiyonunun, -2, -4, -6 … için sıfır olduğu biliniyor. Diğer taraftan, Bernhard Riemann’ın ortaya sürdüğü tez, fonksiyona ait geri kalan tüm sıfırların doğrusu üzerinde kaldığı şeklinde. Bu yargı, henüz kanıtlanamamış olmasına rağmen, sayılar teorisinde önemli bir yer kaplıyor.
Aradan geçen zamanda, hipotez kanıtlanamamış olmasına rağmen, başka veriler ortaya çıktı. Örneğin, 1940’larda, kuantum mekaniği ile, zeta fonksiyonunun sıfırlarının dağılımı arasında ilişkiler olduğu keşfedildi. Örneğin, atomik enerji seviyeleri ve zeta fonksiyonunun sıfırlarının aynı istatistiksel örüntüye uydukları ortaya çıktı. 1999’da ise matematiksel fizik alanında çalışmakta olan Michael Berry ve Jonathan Keiting, David Hilbert ile Gorge Pólya’nın daha önceki bir varsayımlarından hareket ederek, “enerji seviyeleri, Riemann zeta fonksiyonunun aşikâr olmayan sıfırlarına tam olarak denk gelecek bir kuantum sisteminin olduğunu” öne sürdüler. Yani bir enerji seviyeleri \({E_n}\) olmak üzere, \({\zeta _n} = \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/
\kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} + {E_n}i\quad\) olacak şekilde kuantum sistemleri olacağı iddia edildi.
Böylece, bu tür bir kuantum sisteminin varlığının kanıtlanmasının, Riemann zeta hipotezinin de kanıtlanmasında kullanılabileceği için Riemann Hipotezi yarışına fizikçiler de dahil olmuş oldular.
Yakın zamanda ise, Amerika, Kanada ve Birleşik Krallık’tan üç matematikçi, Phsical Review Letters’da yayımlanan makalelerinde, bu aradaki ilişkiyi göstermeye bir adım daha yaklaştıkları ve bu tür bir kuantum sistemini tanımladıkları belirtiliyor. Bundan sonra, eğer bu kuantum sisteminin varlığı gösterilebilirse, bunun aynı zamanda Riemann Hipotezi’nin de kanıtlanması anlamına geleceği söyleniyor.
Şu an ise bilim ve matematik dünyası, uzmanlar tarafından yapılacak yorumları bekliyor.
Riemann zeta fonksiyonu hakkında daha geniş bilgiye buradan ve aşağıdaki videodan ulaşabilirsiniz.
Kaynaklar: Science Alert, Quanta Magazine, Phsical Review Letters